题目内容
设函数f(x)=
,若函数f(x)=2013x的图象上存在点(x0,y0)使得f(f(y0))=y0,求a的取值范围 .
| x+a |
考点:指数函数综合题
专题:函数的性质及应用
分析:由题意可得方程
=y0有正实数根,即 y02-y0-a=0有正实数根.再根据次方程的对称轴为 y0=
,可得△=1+4a≥0,由此解得a的范围.
| y0+a |
| 1 |
| 2 |
解答:
解:f(y0)=y0 一定是f(f(y0))=y0 的实数根,
由于函数f(x)=
在其定义域内是增函数,
函数f(x)=2013x的图象上存在点(x0,y0)使得f(f(y0))=y0,
即方程
=y0有正实数根,
即 y02-y0-a=0有正实数根.
再根据次方程的对称轴为 y0=
,∴△=1+4a≥0,解得 a≥-
,
故答案为:[-
,+∞).
由于函数f(x)=
| x+a |
函数f(x)=2013x的图象上存在点(x0,y0)使得f(f(y0))=y0,
即方程
| y0+a |
即 y02-y0-a=0有正实数根.
再根据次方程的对称轴为 y0=
| 1 |
| 2 |
| 1 |
| 4 |
故答案为:[-
| 1 |
| 4 |
点评:本题主要考查指数函数、二次函数的性质,体现了转化的数学思想,属于中档题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
定义域为R的函数f(x)满足f(x+2)=2f(x),当x∈[0,2]时,f(x)=
,若x∈[-2,0]时,f(x)≥
-
恒成立,则实数t的取值范围是( )
|
| t |
| 2 |
| 1 |
| t |
| A、[-2,0)∪(0,1) |
| B、[-2,0)∪[1,+∞) |
| C、[-2,1] |
| D、(-∞,-2]∪(0,1] |
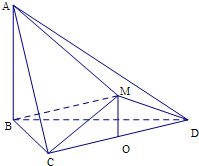 如图,△BCD与△MCD都是边长为2的正三角形,O是CD的中点,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2
如图,△BCD与△MCD都是边长为2的正三角形,O是CD的中点,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2