题目内容
若直线ax-by+1=0平分圆C：x2+y2+2x-4y+1=0的周长，则ab的取值范围是 ．
考点：基本不等式,直线和圆的方程的应用
专题：综合题,不等式的解法及应用,直线与圆
分析：依题意知直线ax-by+1=0过圆C的圆心（-1，2），故有a+2b=1，再利用ab=（1-2b）b=-2（b-
）2+
，求得ab的取值范围．
| 1 |
| 4 |
| 1 |
| 8 |
解答：
解：∵直线ax-by+1=0平分圆C：x2+y2+2x-4y+1=0的周长，
∴直线ax-by+1=0过圆C的圆心（-1，2），
∴有a+2b=1，
∴ab=（1-2b）b=-2（b-
）2+
≤
，
∴ab的取值范围是(-∞，
]．
故答案为：(-∞，
]．
∴直线ax-by+1=0过圆C的圆心（-1，2），
∴有a+2b=1，
∴ab=（1-2b）b=-2（b-
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
∴ab的取值范围是(-∞，
| 1 |
| 8 |
故答案为：(-∞，
| 1 |
| 8 |
点评：本题主要考查直线和圆的位置关系，配方法的应用，属于基础题．
练习册系列答案
相关题目
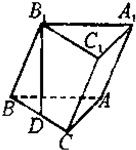如图，已知斜三棱柱ABC-A1B1C1的底面是直角三角形，∠C=90°，侧棱与底面所成的角为α（0°＜α＜90°），点B1在底面上的射影D落在BC上．