题目内容

已知|
p
|=8，|
q
|=6，
p
和
q
的夹角为30°，求|
p
-
q
|的值．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由题意可得
p
•
q
=24
3
，
p
2=64，
q
2=36，再根据|
p
-
q
|=
(
p
-
q
)2
=
p
2+
q
2-2
p
•
q
 计算求得结果．
解答： 解：由题意可得
p
•
q
=8×6×cos30°=24
3
，
p
2=64，
q
2=36，
∴|
p
-
q
|=
(
p
-
q
)2
=
p
2+
q
2-2
p
•
q
=
64+36-48
3
=
100+48
3
．
点评：本题主要考查两个向量的数量积的定义，求向量的模的方法，属于中档题．
练习册系列答案
相关题目
下列说法中错误的是（　　）
A、对于命题p：x0∈R，sin x0＞1，则￢p：x∈R，sin x≤1
B、命题“若0＜a＜1，则函数f（x）=ax在R上是增函数”的逆命题为假命题
C、若p∨q为真命题，则p，q均为真命题
D、命题“若x2-x-2=0，则x=2”的逆否命题是“若x≠2，则x2-x-2≠0”
请画出如图几何体的三视图．
已知非负数a、b、c满足a+b+c=1，证明：
ab
c+1
+
bc
a+1
+
ca
b+1
≤
1
4
．
设各项均为正数的数列{an}和{bn}满足：an，bn，an+1成等差数列，bn，an+1，bn+1成等比数列，且a1=1，b1=2，a2=3，求通项an，bn．
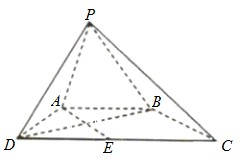如图，在四棱锥P-ABCD中，AB∥CD，△PAB和△PAD是两个边长为2的正三角形．DC=4，PD⊥PB，点E在线段CD上．
（Ⅰ）当
DE
EC
为何值时，AE⊥面PBD：
（Ⅱ）求直线CB与平面PDC所成角的正弦值．
已知函数f（x）=x2-ax+2，g（x）=aln（x-1）-2a+6（a为常数），
（1）当x∈[2，+∞）时f（x）≥g（x）恒成立，求实数a的取值范围；
（2）若函数h（x）=xf（x）有对称中心为A（1，0），求证：函数h（x）的切线L在切点处穿过h（x）图象的充要条件是L恰为函数在点A处的切线．（直线穿过曲线是指：直线与曲线有交点，且在交点左右附近曲线在直线异侧）
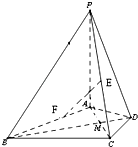在四棱锥P-ABCD中，PA⊥平面ABCD，△ABC是正三角形，AC与BD的交点M恰好是AC中点，又PA=AB=4，∠CDA=120°．
（1）求证：BD⊥PC；
（2）设E为PC的中点，点F在线段AB上，若直线EF∥平面PAD，求AF的长；
（3）求二面角A-PC-B的余弦值．
设函数f(x)=
x+a
，若函数f（x）=2013x的图象上存在点（x0，y0）使得f（f（y0））=y0，求a的取值范围
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网