题目内容

已知点A（-1，1）、B（1，2）、C（-2，1）、D（3，4），则向量
AB
在
CD
方向上的投影为
 
．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用平面向量的数量积、向量的投影定义即可得出．
解答： 解：∵
AB
=(2，1)，
CD
=（5，3）．
设
AB
与
CD
夹角为θ，
则cosθ=
AB
•
CD
|
AB
| |
CD
|
=
10+3
5
×
34
，
∴向量
AB
在
CD
方向上的投影为
AB
cosθ=
5
×
13
5
×
34
=
13
34
34
．
故答案为：
13
34
34
．
点评：本题考查了平面向量的数量积、向量的投影，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=x2-ax+2，g（x）=aln（x-1）-2a+6（a为常数），
（1）当x∈[2，+∞）时f（x）≥g（x）恒成立，求实数a的取值范围；
（2）若函数h（x）=xf（x）有对称中心为A（1，0），求证：函数h（x）的切线L在切点处穿过h（x）图象的充要条件是L恰为函数在点A处的切线．（直线穿过曲线是指：直线与曲线有交点，且在交点左右附近曲线在直线异侧）
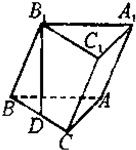如图，已知斜三棱柱ABC-A1B1C1的底面是直角三角形，∠C=90°，侧棱与底面所成的角为α（0°＜α＜90°），点B1在底面上的射影D落在BC上．
（1）求证：AC⊥平面BB1C1C；
（2）当α为何值时，AB1⊥BC1，且使点D恰为BC中点？
（3）（理科做）当α=arccos
1
3
，且AC=BC=AA1时，求二面角C1-AB-C的大小．
设函数f(x)=
x+a
，若函数f（x）=2013x的图象上存在点（x0，y0）使得f（f（y0））=y0，求a的取值范围
 
．
将边长为1的正方形ABCD沿对角线BD折成直二面角，则二面角B-AC-D的余弦值为
 
．
若（2x+
a
x
）4（a＞0）的展开式中常数项为96，则实数a等于
 
．
若圆锥底面半径为1，高为2，则圆锥的侧面积为
 
．
设m，n是两条不同的直线，α，β，γ是三个不同的平面，给出下列四个命题：
①若m⊥α，n⊥α，则m⊥n；②若α∥β，β∥γ，m⊥α，则m⊥γ；
③若m∥α，n∥α，则m∥n；④若α⊥γ，β⊥γ，则α∥β．
其中正确命题的序号是
 
．
双曲线
x2
4
-y2=1的焦点到渐近线的距离为（　　）
A、2
B、
2
C、1
D、3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网