题目内容
一个几何体的三视图如图所示,已知这个几何体的体积为10
,则h= .

| 3 |

考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:根据三视图判断几何体是四棱锥,且四棱锥的一条侧棱与底面垂直,高为h,四棱锥的底面为矩形,矩形的长和宽分别为5和6;把数据代入棱锥的体积公式,根据体积为10
求出h.
| 3 |
解答:
解:由三视图知几何体四棱锥,且四棱锥的一条侧棱与底面垂直,高为h,
四棱锥的底面为矩形,矩形的长和宽分别为5和6;
则几何体的体积V=
×5×6×h=10
,
∴h=
.
故答案为:
.
四棱锥的底面为矩形,矩形的长和宽分别为5和6;
则几何体的体积V=
| 1 |
| 3 |
| 3 |
∴h=
| 3 |
故答案为:
| 3 |
点评:本题考查了由三视图求几何体的体积,判断几何体的形状及数据所对应的几何量是解答此类问题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
若函数f(x)=2sin(
x+
)(-2<x<14)的图象与x轴交于点A,过点A的直线l与函数的图象交于B、C两点,则(
+
)•
=(其中O为坐标原点)( )
| π |
| 8 |
| π |
| 4 |
| OB |
| OC |
| OA |
| A、-32 | B、32 |
| C、-72 | D、72 |
函数y=ln(x+1)与y=
的图象交点的横坐标所在区间为( )
| 1 |
| x |
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
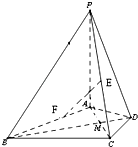 在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°.
在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°.