题目内容
4.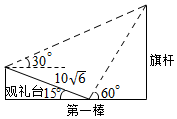 如图,在坡角(坡面与水平面的夹角)为15°的观礼台上,某一列座位与旗杆在同一个垂直于地面的平面上,在该列的第一排和最后一排测得旗杆的仰角分别为60°和30°,且第一排和最后一排的距离10$\sqrt{6}$米,则旗杆的高度为30米.
如图,在坡角(坡面与水平面的夹角)为15°的观礼台上,某一列座位与旗杆在同一个垂直于地面的平面上,在该列的第一排和最后一排测得旗杆的仰角分别为60°和30°,且第一排和最后一排的距离10$\sqrt{6}$米,则旗杆的高度为30米.
分析 求出△ACD的各角,利用正弦定理解出AD,则AB=ADsin60°.
解答 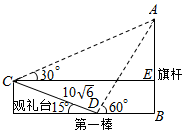 解由已知得∠ACD=30°+15°=45°,∠ADC=180°-60°-15°=105°,∴∠CAD=30°.
解由已知得∠ACD=30°+15°=45°,∠ADC=180°-60°-15°=105°,∴∠CAD=30°.
在△ACD中,由正弦定理得$\frac{CD}{sin∠CAD}=\frac{AD}{sin∠ACD}$,
即$\frac{10\sqrt{6}}{\frac{1}{2}}=\frac{AD}{\frac{\sqrt{2}}{2}}$,解得AD=20$\sqrt{3}$.
∴AB=AD•sin∠ADB=20$\sqrt{3}×\frac{\sqrt{3}}{2}$=30(米)
故答案为:30.
点评 本题考查了正弦定理在解三角形中的应用,属于中档题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
19.已知全集U=R,集合A={x|-2≤x<0},B={x|2x-1<$\frac{1}{4}$},则A∩B=( )
| A. | (-∞,-2)∪(-1,+∞) | B. | (-∞,-2)∪[-1,+∞) | C. | [-2,-1) | D. | (-2,+∞) |
9.某超市某种面包进货价为每个4元,实际售价为每个4.5元,若当天不能卖完,就在闭店前以每个3元的价格全部处理,据以往统计日需求量(单位:个)的情况如表:
若某日超市面包进货量为600.
(1)若以日需求量x所在区间的中间值为估计值,根据上表列出当日利润y的分布列;
(2)估计超市当日利润y的均值.
| 日需求量x | (0,400] | (400,600] | (600,800] | (800,1000] |
| 频率 | 0.2 | 0.4 | 0.3 | 0.1 |
(1)若以日需求量x所在区间的中间值为估计值,根据上表列出当日利润y的分布列;
(2)估计超市当日利润y的均值.
14.记不等式组$\left\{\begin{array}{l}{x≥0}\\{x+3y≥4}\\{3x+y≤4}\end{array}\right.$所表示的平面区域为D,若直线y=a(x+1)与区域D有公共点,则实数a的取值范围为( )
| A. | ($\frac{1}{2}$,$\frac{4}{3}$) | B. | [$\frac{4}{3}$,4] | C. | [$\frac{4}{3}$,3) | D. | [$\frac{1}{2}$,4] |
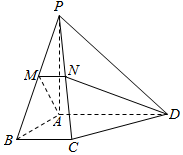 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=2BC=2,过AD的平面分别交PB,PC于M,N两点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=2BC=2,过AD的平面分别交PB,PC于M,N两点.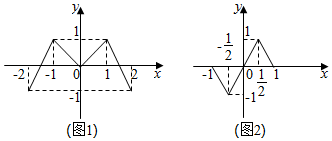 已知偶函数f(x),奇函数g(x)的图象分别如图(1)、图(2)所示,若f(y0)=0且y0=g(x0),则x0的值为-1,0,或1.
已知偶函数f(x),奇函数g(x)的图象分别如图(1)、图(2)所示,若f(y0)=0且y0=g(x0),则x0的值为-1,0,或1.