题目内容
13.已知函数f(x)的定义域为R,且为可导函数,若对?x∈R,总有(2-x)f(x)+xf′(x)<0成立(其中f′(x)是f(x)的导函数),则( )| A. | f(x)>0恒成立 | B. | f(x)<0恒成立 | ||
| C. | f(x)的最大值为0 | D. | f(x)与0的大小关系不确定 |
分析 求出函数的导数,解关于导函数的不等式,求出函数的最大值小于0,从而证出结论
解答 解:设g(x)=$\frac{{x}^{2}f(x)}{{e}^{x}}$
∴g′(x)=$\frac{x[(2-x)f(x)+xf′(x)]}{{e}^{x}}$,
∵对?x∈R,总有(2-x)f(x)+xf′(x)<0成立,
当x>0时,g′(x)<0,函数g(x)递减
当x<0时,g′(x)>0,函数g(x)递增,
∴g(x)<g(0)=0,
∴$\frac{{x}^{2}f(x)}{{e}^{x}}$<0恒成立
∴f(x)<0恒成立,
故选:B
点评 本题考查了函数的单调性问题,考查导数的应用,构造函数g(x)是解题的关键,本题是一道中档题.

练习册系列答案
相关题目
1.下列语句是假命题的是( )
| A. | 正方形的四条边相等 | B. | 若x=0,则xy=0 | ||
| C. | $\sqrt{3}∈N$ | D. | 负数的平方是正数 |
8.如果方程Ax+By+C=0表示的直线是x轴,则A、B、C满足( )
| A. | A•C=0 | B. | B≠0 | C. | B≠0且A=C=0 | D. | A•C=0且B≠0 |
5.如图,正四面体ABCD的棱长为1,点E是棱CD的中点,则$\overrightarrow{AE}$•$\overrightarrow{AB}$=( )
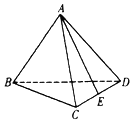

| A. | -$\frac{1}{4}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |