题目内容
4.设$f(x)={sin^2}x+\sqrt{3}sinxcosx-\frac{1}{2}(x∈R)$.(1)求函数f(x)的最小正周期与值域;
(2)设△ABC内角A,B,C的对边分别为a,b,c,A为锐角,$a=2\sqrt{3},c=4$,若f(A)=1,求A,b.
分析 (1)利用三角函数恒等变换的应用化简函数解析式可得f (x)=sin(2x-$\frac{π}{6}$)(x∈R),利用正弦函数的性质即可求解.
(2)由题意可得sin(2A-$\frac{π}{6}$)=1.由A为锐角,可求2A-$\frac{π}{6}$∈(-$\frac{π}{6}$,$\frac{5π}{6}$),利用正弦函数的性质可求A的值,进而利用余弦定理解得b的值.
解答 (本题满分14分)
解:(1)化简得:f (x)=sin(2x-$\frac{π}{6}$)(x∈R),
所以最小正周期为π,值域为[-1,1].…(7分)
(2)因为f (A)=sin(2A-$\frac{π}{6}$)=1.
因为A为锐角,
所以2A-$\frac{π}{6}$∈(-$\frac{π}{6}$,$\frac{5π}{6}$),
所以2A-$\frac{π}{6}$=$\frac{π}{2}$,
所以A=$\frac{π}{3}$.
由余弦定理a2=b2+c2-2bccosA,
得b2-4b+4=0.解得b=2.…(14分)
点评 本题主要考查了三角函数恒等变换的应用,利用正弦函数的性质,余弦定理在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
19.已知直线2x+y-2=0经过椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>0,b>0)$的上顶点与右焦点,则椭圆的方程为( )
| A. | $\frac{x^2}{5}+\frac{y^2}{4}=1$ | B. | $\frac{x^2}{4}+{y^2}=1$ | C. | $\frac{x^2}{9}+\frac{y^2}{4}=1$ | D. | $\frac{x^2}{6}+\frac{y^2}{4}=1$ |
9.在原命题及其逆命题、否命题、逆否命题中,真命题的个数可以是( )
| A. | 1或2或3或4 | B. | 0或2或4 | C. | 1或3 | D. | 0 |
13.已知函数f(x)的定义域为R,且为可导函数,若对?x∈R,总有(2-x)f(x)+xf′(x)<0成立(其中f′(x)是f(x)的导函数),则( )
| A. | f(x)>0恒成立 | B. | f(x)<0恒成立 | ||
| C. | f(x)的最大值为0 | D. | f(x)与0的大小关系不确定 |
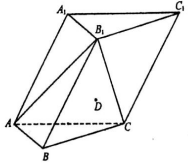 如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,∠A1AC=60°.
如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,∠A1AC=60°.