题目内容
若x，y∈R，函数f（x）=（x+y）2+（
-y）2的最小值是（ ）
| 1 |
| x |
| A、4 | B、0 | C、2 | D、1 |
考点：基本不等式
专题：计算题,不等式的解法及应用
分析：f（x）=（x+y）2+（
-y）2表示（x，
）与（-y，y）两点间距离的平方，则问题转化为求曲线y=
上的点到y=-x上的点的距离的最小值的平方，由曲线的性质可求答案．
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
解答：
解：f（x）=（x+y）2+（
-y）2表示（x，
）与（-y，y）两点间距离的平方，
则问题转化为求曲线y=
上的点到y=-x上的点的距离的最小值的平方，
而两曲线关于y=x对称，
∴（1，1）或（-1，-1）到（0，0）的距离的平方即为所求，
d=
2=2，
故选：C．
| 1 |
| x |
| 1 |
| x |
则问题转化为求曲线y=
| 1 |
| x |
而两曲线关于y=x对称，
∴（1，1）或（-1，-1）到（0，0）的距离的平方即为所求，
d=
| 2 |
故选：C．
点评：该题考查函数的最值问题，考查转化思想，解决该题的关键是熟练式子的几何意义并能正确转化．
练习册系列答案
相关题目
设函数f（x）=xa+1（a∈Q）的定义域为[-b，-a]∪（a，b]，其中0＜a＜b，且f（x）在[a，b]上的最大值为6，最小值为3，则f（x）在[-b，-a]上的最大值与最小值的和是（ ）
| A、-5 | B、9 |
| C、-5或9 | D、以上不对 |
函数y=|x+1|+2的最小值是（ ）
| A、0 | B、-1 | C、2 | D、3 |
设函数f（x）=
在x=0处f（x）（ ）
|
| A、不连续 |
| B、连续，但不可导 |
| C、可导，但导数不连续 |
| D、可导，且导数连续 |
函数f（x）=x3-3x-1的单调减区间是（ ）
| A、（-∞，-1） |
| B、（-1，1） |
| C、（1，+∞） |
| D、（-∞，-1）和（1，+∞） |
已知直线a和平面α，则能推出a∥α的是（ ）
| A、存在一条直线b，a∥b，且b∥α |
| B、存在一条直线b，a⊥b，且b⊥α |
| C、存在一个平面β，a?β，且α∥β |
| D、存在一个平面β，a∥β，且α∥β |
已知函数y=f（x）的导函数y=f′（x）的图象如图，则（ ）
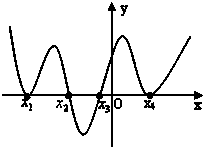
| A、函数f（x）有2个极大值点，2个极小值点 |
| B、函数f（x）有1个极大值点，1个极小值点 |
| C、函数f（x）有3个极大值点，1个极小值点 |
| D、函数f（x）有1个极大值点，3个极小值点． |