题目内容
用1、2、3、4、5、6这六个数字组成无重复数字的四位数,求:
(1)奇数数字必须在奇数位的有多少个?
(2)奇数位只排奇数数字的有多少个?
(1)奇数数字必须在奇数位的有多少个?
(2)奇数位只排奇数数字的有多少个?
考点:计数原理的应用
专题:排列组合
分析:(1)奇数数字必须在奇数位的:
有三类:①3个奇数,1个偶数,②2个奇数,2个偶数,③1个奇数,3个偶数,再按要求排列即可得出总数.
(2)每位分别选择:千位任选奇数
,十位在剩下的两个奇数里任选
,然后剩下百位和个位任选,分别是
和
,即可求解总数.
有三类:①3个奇数,1个偶数,②2个奇数,2个偶数,③1个奇数,3个偶数,再按要求排列即可得出总数.
(2)每位分别选择:千位任选奇数
| C | 1 3 |
| C | 1 2 |
| C | 1 4 |
| C | 1 3 |
解答:
解:(1)奇数数字必须在奇数位的:
可以有三类:①3个奇数,1个偶数,
先选择1个偶数,3个奇数,
×
=3,
再按要求排列:
×
=12,
∴共有3×12=36个,
②2个奇数,2个偶数,
先选择2个偶数,2个奇数,
×
=9;
再按要求排列:
×
=4,
共有9×4=36个,
③1个奇数,3个偶数,
先选择1个偶数,3个奇数,
×
=3,
再按要求排列:
×
=12,
∴共有3×12=36个,
总共符合题意的有36×3=108,
即奇数数字必须在奇数位的有108个.
(2)∵奇数位只排奇数数字,偶数位置可以奇数偶数都可以,
千位任选奇数
,十位在剩下的两个奇数里任选
,然后剩下百位和个位可以从剩下的4个数中选择,分别是
和
,
∴一共
×
×
×
=72(个)
即奇数位只排奇数数字的72个.
可以有三类:①3个奇数,1个偶数,
先选择1个偶数,3个奇数,
| C | 1 3 |
| C | 3 3 |
再按要求排列:
| A | 2 3 |
| A | 2 2 |
∴共有3×12=36个,
②2个奇数,2个偶数,
先选择2个偶数,2个奇数,
| C | 2 3 |
| C | 2 3 |
再按要求排列:
| A | 2 2 |
| A | 2 2 |
共有9×4=36个,
③1个奇数,3个偶数,
先选择1个偶数,3个奇数,
| C | 1 3 |
| C | 3 3 |
再按要求排列:
| A | 1 2 |
| A | 3 3 |
∴共有3×12=36个,
总共符合题意的有36×3=108,
即奇数数字必须在奇数位的有108个.
(2)∵奇数位只排奇数数字,偶数位置可以奇数偶数都可以,
千位任选奇数
| C | 1 3 |
| C | 1 2 |
| C | 1 4 |
| C | 1 3 |
∴一共
| C | 1 3 |
| C | 1 2 |
| C | 1 4 |
| C | 1 3 |
即奇数位只排奇数数字的72个.
点评:本题考查了排列组合的知识,分类思想,注意语言的区别,确定的方法,以什么为标准,是解本题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
满足M⊆{a1,a2,a3},且M∩{a1,a2,a3}={a3}的集合M的子集个数是( )
| A、1 | B、2 | C、3 | D、4 |
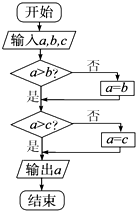 如图所示的算法中,令a=tan θ,b=sin θ,c=cos θ,若在集合{θ|-
如图所示的算法中,令a=tan θ,b=sin θ,c=cos θ,若在集合{θ|-