圆柱被一个平面截去一部分后与一个四棱锥组成的几何体的三视图如图所示.则该几何体的体积为( )A．4π+8B．8π+16C．16π+16D．16π+48 题目和参考答案——青夏教育精英家教网—

题目内容

15．圆柱被一个平面截去一部分后与一个四棱锥组成的几何体的三视图如图所示，则该几何体的体积为（　　）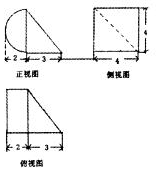

A．

4π+8

B．

8π+16

C．

16π+16

D．

16π+48

分析由已知中的三视图，可得该几何体是一个半圆柱与四棱锥的组合体，分别计算体积可得答案．

解答解：由已知中的三视图，可得该几何体是一个半圆柱与四棱锥的组合体，
半圆柱的底面半径为2，高为4，故体积为：$\frac{1}{2}π•{2}^{2}•4$=8π，
四棱锥的底面面积为：4×4=16，高为3，故体积为：16，
故组合体的体积V=8π+16，
故选：B

点评本题考查的知识点是圆柱的体积和表面积，棱锥的体积和表面积，简单几何体的三视图，难度中档．

练习册系列答案

6．在-1和7中间插入三个数，使得这五个数成单调递增的等差数列，则这三个数为1，3，5．

3．在△ABC中，角A，B，C的对边分别为a，b，c，且bc=a²-（b-c）²．
（1）求角A的大小；
（2）若a=2$\sqrt{3}$，△ABC的面积S=2$\sqrt{3}$，求b，c的值．

10．在空间直角坐标系O-xyz中，若O（0，0，0），A（0，2，0），B（2，0，0），C（2，2，2$\sqrt{3}$），则二面角C-OA-B的大小为（　　）

20．已知直线l₁：ax+4y-1=0，l₂：x+ay-$\frac{1}{2}$=0，若l₁∥l₂，则实数a=-2．

7．

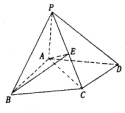在四棱锥P-ABCD中，△ABC为正三角形，AB⊥AD，AC⊥CD，PA⊥平面ABCD，PC与平面ABCD所成角为45°
（1）若E为PC的中点，求证：PD⊥平面ABE；
（2）若CD=$\sqrt{3}$，求点B到平面PCD的距离．

4．设集合M={x|2^x+1＞1}，N={x|lnx≤1}，则M∩N等于（　　）

5．设命题P：?n∈N，n²＜2ⁿ，则￢P为（　　）

试题分类