题目内容
9.已知0<a<b,且a+b=1,则下列不等式中正确的是( )| A. | log2a>0 | B. | 2a-b<$\frac{1}{2}$ | C. | log2a+log2b<-2 | D. | 2($\frac{a}{b}$+$\frac{b}{a}$)<$\frac{1}{2}$ |
分析 利用基本不等式的性质依次判断即可.
解答 解:对于A:log2a>0可得log2a>log21,∵0<a<b,且a+b=1,即a<1,故A不对.
对于B:2a-b<$\frac{1}{2}$可得:2a-b<2-1,即a-b<-1,可得a+1<b,与a+b=1矛盾,故B不对.
对于C:log2a+log2b<-2可得:log2ab<-2,即∵ab$<\frac{1}{4}$,∵0<a<b,且a+b=1,1=a+b>2$\sqrt{ab}$,可得ab<$\frac{1}{4}$,故C对.
对于D:2($\frac{a}{b}$+$\frac{b}{a}$)<$\frac{1}{2}$,∵0<a<b,且a+b=1,$\frac{a}{b}+\frac{b}{a}>2$,故D不对.
故选:C.
点评 本题考查了基本不等式的性质,考查了灵活解决问题的能力,属于基础题.

练习册系列答案
相关题目
19.已知函数f(x)=ln$\frac{x}{2}$+$\frac{1}{2}$,g(x)=ex-2,对?m∈R,?n∈(0,+∞)使得g(m)=f (n)成立,则n-m的最小值为( )
| A. | -ln 2 | B. | ln 2 | C. | 2$\sqrt{e}$-3 | D. | e2-3 |
17.已知平面向量$\vec a,\vec b$的夹角为$60°,\vec a=({\sqrt{3},1}),|\vec b|=1$则$|\vec a+2\vec b|$=( )
| A. | 2 | B. | $\sqrt{7}$ | C. | $2\sqrt{7}$ | D. | $2\sqrt{3}$ |
1.已知正方形ABCD的边长为2,E为CD的中点,则$\overrightarrow{AE}•\overrightarrow{CB}$=( )
| A. | -4 | B. | -3 | C. | 4 | D. | $2\sqrt{5}$ |
9.某市在一次降雨过程中,降雨量y(mm)与时间t(min)的函数关系可近似地表示为y=f(t)=$\sqrt{t}$,则在时刻t=40min的降雨强度为( )
| A. | 40mm | B. | 40$\sqrt{10}$mm | C. | $\frac{1}{40}$mm/min | D. | $\frac{\sqrt{10}}{40}$mm/min |
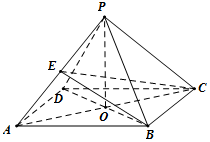 在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,AC∩BD=O.
在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,AC∩BD=O.