题目内容
20.某几何体的三视图如图所示,则该几何体的体积为( )
| A. | 5 | B. | $\frac{16}{3}$ | C. | 7 | D. | $\frac{17}{3}$ |
分析 由已知中的三视图,可知该几何体是一个正方体切去一个底面边长为1的直角三角形,高为2的三棱锥和切去一个底面为边长为1和2的直角三角形,高为2的三棱柱.从而可得该几何体的体积.
解答 解:由已知的三视图,可知该几何体是一个正方体切去一个底面边长为1的直角三角形,高为2的三棱锥和切去一个底面为边长为1和2的直角三角形,高为2的三棱柱.从而可得该几何体的体积.
∴三棱锥的体积$V=\frac{1}{3}×\frac{1}{2}×1×1×2=\frac{1}{3}$,
三棱柱的体积$V=\frac{1}{2}×1×2×2=2$.
正方体的体积V=2×2×2=8.
故得:该几何体的体积$V=8-2-\frac{1}{3}=\frac{17}{3}$.
故选D.
点评 本题主要考查了三视图的投影的认识和体积的计算.属于基础题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
10.在空间直角坐标系O-xyz中,若O(0,0,0),A(0,2,0),B(2,0,0),C(2,2,2$\sqrt{3}$),则二面角C-OA-B的大小为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
11. 秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出v的值为( )
秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出v的值为( )
 秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出v的值为( )
秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出v的值为( )| A. | 210-1 | B. | 210 | C. | 310-1 | D. | 310 |
8.一个圆锥的底面圆半径为3,高为4,则这个圆锥的侧面积为( )
| A. | $\frac{15π}{2}$ | B. | 24π | C. | 15π | D. | 20π |
5.设命题P:?n∈N,n2<2n,则¬P为( )
| A. | ?n∈N,n2<2n | B. | ?n∈N,n2≥2n | C. | ?n∈N,n2≥2n | D. | ?n∈N,n2>2n |
12.定义在R上的偶函数f(x)的导函数为f'(x),若对任意的实数x,都有2f(x)+xf'(x)<2恒成立,则使x2f(x)-4f(2)<x2-4成立的实数x的取值范围是( )
| A. | (-∞,-2)∪(2,+∞) | B. | (-2,0)∪(0,2) | C. | {x|x≠±2} | D. | (-2,2) |
9.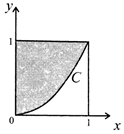 在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C的方程为x2-y=0)的点的个数的估计值为( )
在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C的方程为x2-y=0)的点的个数的估计值为( )
 在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C的方程为x2-y=0)的点的个数的估计值为( )
在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C的方程为x2-y=0)的点的个数的估计值为( )| A. | 5000 | B. | 6667 | C. | 7500 | D. | 7854 |
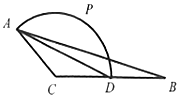 已知△ABC中,AC=2,BC=4,AB=2$\sqrt{7}$,且D是BC的中点.
已知△ABC中,AC=2,BC=4,AB=2$\sqrt{7}$,且D是BC的中点.