题目内容
已知椭圆C:
+
=1(a>b>0),过椭圆C的右焦点F的直线l交椭圆于A,B两点,交y轴于P点,设
=m
,
=n
,(m,n∈R).已知椭圆C上的点到焦点F的最大值与最小值的比值为3+2
.
(1)求椭圆的离心率;
(2)求证:m+n为定值.
| x2 |
| a2 |
| y2 |
| b2 |
| PA |
| AF |
| PB |
| BF |
| 2 |
(1)求椭圆的离心率;
(2)求证:m+n为定值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件推导出
=3+2
,由此能求出椭圆的离心率.
(2)由 (1)得a2=2c2,b2=c2,设椭圆方程为
+
=1,直线方程为:y=k(x-c),由
,得(2k2+1)x2-4k2cx+2k2c-2c2=0,由此利用韦达定理结合已知条件能证明m+n为定值.
| a+c |
| a-c |
| 2 |
(2)由 (1)得a2=2c2,b2=c2,设椭圆方程为
| x2 |
| 2c2 |
| y2 |
| c2 |
|
解答:
(1)解:∵椭圆C上的点到焦点F的最大值与最小值的比值为3+2
,
∴
=3+2
,
∴
=3+2
,
解得e=
,
∴椭圆的离心率为
.
(2)证明:由 (1)得a2=2c2,b2=c2,
设椭圆方程为
+
=1,
直线方程为:y=k(x-c),A(x1,y1),B(x2,y2)
由
,得(2k2+1)x2-4k2cx+2k2c-2c2=0,
∴x1+x2=
,x1x2=
,
又点P(0,-kc),
由
=m
,
=n
,(m,n∈R),
得m=
,n=
,
∴m+n=
+
=
=-4.
∴m+n为定值-4.
| 2 |
∴
| a+c |
| a-c |
| 2 |
∴
| 1+e |
| 1-e |
| 2 |
解得e=
| ||
| 2 |
∴椭圆的离心率为
| ||
| 2 |
(2)证明:由 (1)得a2=2c2,b2=c2,
设椭圆方程为
| x2 |
| 2c2 |
| y2 |
| c2 |
直线方程为:y=k(x-c),A(x1,y1),B(x2,y2)
由
|
∴x1+x2=
| 4k2c |
| 2k2+1 |
| 2k2c2-2c2 |
| 2k2+1 |
又点P(0,-kc),
由
| PA |
| AF |
| PB |
| BF |
得m=
| x1 |
| c-x1 |
| x2 |
| c-x2 |
∴m+n=
| x1 |
| c-x1 |
| x2 |
| c-x2 |
| c(x1+x2)-2x1x2 |
| c2-c(x1+x2)+x1x2 |
∴m+n为定值-4.
点评:本题考查椭圆的离心率的求法,考查两数和为定值的证明,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
复数
的虚部是( )
| 5i |
| 1+2i |
| A、1 | B、-1 | C、i | D、-i |
若复数z满足zi=4-5i(其中i为虚数单位),则复数z为( )
| A、5-4i | B、-5+4i |
| C、5+4i | D、-5-4i |
将1,2,3,4四个数分为两组,每组至少一个数,则两组数的和相等的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在二项式(x-
)n的展开式中恰好第5项的二项式系数最大,则展开式中含x2项的系数是( )
| 1 |
| x |
| A、-56 | B、-35 |
| C、35 | D、56 |
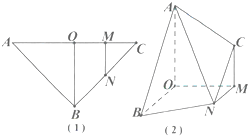 如图(1),在三角形ABC中,BA=BC=2
如图(1),在三角形ABC中,BA=BC=2