题目内容
若关于x的方程x2-2x+a=0在(
,3)上恰有2个不相等的实数根,则实数a的取值范围是 .
| 1 |
| 2 |
考点:一元二次方程的根的分布与系数的关系
专题:计算题,函数的性质及应用
分析:构造f(x)=x2-2x+a=(x-1)2-1+a,根据关于x的方程x2-2x+a=0在(
,3)上恰有2个不相等的实数根,可得
,即可求出实数a的取值范围.
| 1 |
| 2 |
|
解答:
解:函数f(x)=x2-2x+a=(x-1)2-1+a
∴函数f(x)的图象开口向上,对称轴x=1
根据题意可知:
,
解得:
<a<1.
故答案为:
<a<1.
∴函数f(x)的图象开口向上,对称轴x=1
根据题意可知:
|
解得:
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:本题考查一元二次方程的根的分布与系数的关系,考查函数与方程思想的运用,属于中档题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
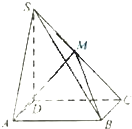 如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=
如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=