题目内容
参数方程
（θ为参数）表示的曲线是（ ）
|
| A、圆 | B、直线 | C、线段 | D、射线 |
考点：参数方程化成普通方程
专题：坐标系和参数方程
分析：将参数方程中两式相减，即可得到y=x+1，同时注意x的范围是[-1，1]，即可得到结果．
解答：
解：参数方程
（θ为参数），化为普通方程为：
y=1+x（-1≤x≤1），
故表示的曲线为线段．
故选C．
|
y=1+x（-1≤x≤1），
故表示的曲线为线段．
故选C．
点评：本题主要考查参数方程化为普通方程，注意等价性，即x的范围，是一道基础题．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
已知数列{an}的前n项和Sn=n2+
，则（ ）
| 2 |
| 3 |
| A、an=2n-1 | |||||||
| B、an=2n+1 | |||||||
C、an=
| |||||||
D、an=
|
下列函数中增加得最快的是（ ）
| A、y=2x |
| B、y=3x |
| C、y=4x |
| D、y=ex |
下列说法正确的是（ ）
| A、小于90°的角是锐角 |
| B、大于90°的角是钝角 |
| C、0°～90°间的角一定是锐角 |
| D、锐角一定是第一象限的角 |
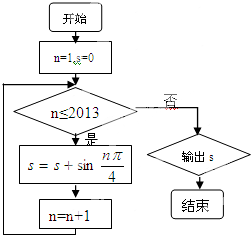
一个算法的程序框图如图，则其输出结果是（ ）
| A、0 | ||||
B、
| ||||
C、
| ||||
D、
|
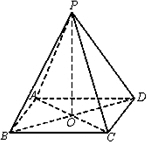如图，在四棱锥P-ABCD中，底面ABCD是矩形，四条侧棱长均相等且BD交AC于点O．