题目内容
若复数Z满足(3-2i)Z=|4+3i|,则Z的虚部为( )
A、
| ||
B、-
| ||
C、-
| ||
D、
|
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:根据复数的基本运算以及复数的模长公式进行化简即可.
解答:
解:由(3-2i)Z=|4+3i|,得(3-2i)Z=5,
即Z=
=
=
=
+
i,
故Z的虚部为
,
故选:A
即Z=
| 5 |
| 3-2i |
| 5(3+2i) |
| (3-2i)(3+2i) |
| 15+10i |
| 9+4 |
| 15 |
| 13 |
| 10 |
| 13 |
故Z的虚部为
| 10 |
| 13 |
故选:A
点评:本题主要考查复数的基本运算,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在等差数列{an}中an>0,且a1+a2+a3+…+a8=40,则a4•a5的最大值是( )
| A、5 | B、10 |
| C、25 | D、AB=4,50 |
已知(0.81.8)a>(1.80.8)a,则a的取值范围是( )
| A、(0,+∞) |
| B、(-∞,0) |
| C、(1,+∞) |
| D、(-∞,1) |
若
=-
,则
的值是( )
| 1+sinx |
| cosx |
| 1 |
| 2 |
| cosx |
| sinx-1 |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
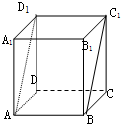 如图,正方体ABCD-A1B1C1D1中,平面ABC1D1与平面ABCD所成二面角的大小为( )
如图,正方体ABCD-A1B1C1D1中,平面ABC1D1与平面ABCD所成二面角的大小为( )| A、300 |
| B、450 |
| C、600 |
| D、900 |