题目内容
已知x∈(0,
),化简:
+
.
| π |
| 2 |
1+2sin
|
1-2sin
|
考点:三角函数的化简求值
专题:三角函数的求值
分析:由角的范围可推出sinθ<cosθ,以及sinθ+cosθ<0,化简要求的式子,求得最简结果即可.
解答:
解:x∈(0,
),∴
∈(0,
),cos
>sin
.
∴
+
=sin
+cos
+|sin
-cos
|
=sin
+cos
-sin
+cos
=2cos
| π |
| 2 |
| x |
| 2 |
| π |
| 4 |
| x |
| 2 |
| x |
| 2 |
∴
1+2sin
|
1-2sin
|
=sin
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
=sin
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
=2cos
| x |
| 2 |
点评:本题主要考查同角三角函数的基本关系,二倍角公式的应用,属于中档题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
函数f(x)=sin(2x+φ)(|φ<
|)的图象向左平移
个单位后关于原点对称,求函数f(x)在[0,
]上的最小值为( )
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
已知a,b为非零实数,若a>b且ab>0,则下列不等式成立的是( )
| A、a2>b2 | ||||
B、
| ||||
| C、ab2>a2b | ||||
D、
|
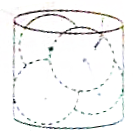 如图,在底面直径为4r的圆柱内,正方放入4个半径为r的小球,使得圆柱上下表面与小球正好相切,则圆柱的高为
如图,在底面直径为4r的圆柱内,正方放入4个半径为r的小球,使得圆柱上下表面与小球正好相切,则圆柱的高为