题目内容
10．设抛物线y2=8x的焦点为F，过F作倾斜角为60°的直线交抛物线于A，B两点（点A在第一象限），与其准线交于点C，则$\frac{{S}_{△AOC}}{{S}_{△BOF}}$=（ ）| A． | 6 | B． | 7 | C． | 8 | D． | 10 |
分析 由题意，直线的方程为y=$\sqrt{3}$（x-2），代入y2=8x可得3x2-20x+12=0，求出A，B的坐标，再求出C的坐标，即可求出$\frac{{S}_{△AOC}}{{S}_{△BOF}}$．
解答 解：由题意，直线的方程为y=$\sqrt{3}$（x-2），
代入y2=8x可得3x2-20x+12=0，∴x=6或$\frac{2}{3}$，
∴A（6，4$\sqrt{3}$），B（$\frac{2}{3}$，$\frac{4\sqrt{3}}{3}$），
又抛物线的准线方程为x=-2，∴C（-2，-4$\sqrt{3}$），
∴$\frac{{S}_{△AOC}}{{S}_{△BOF}}$=$\frac{\frac{1}{2}•2•8\sqrt{3}}{\frac{1}{2}•2•\frac{4\sqrt{3}}{3}}$=6，
故选：A．
点评 本题考查直线与抛物线的位置关系，考查抛物线的性质，考查三角形面积的计算，确定A，B，C的坐标是关键．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
1．设数列{an}的通项公式为an=3n，且a2，a4，ak成等比数列，则数列k的值为（ ）
| A． | 9 | B． | 8 | C． | 7 | D． | 6 |
18．已知在△ABC中，cos2C=$\frac{1}{3}$，cos（A-B）=$\frac{\sqrt{3}}{4}$，且c=asinB，则cosAcosB=（ ）
| A． | -$\frac{\sqrt{3}}{12}$ | B． | $\frac{\sqrt{3}}{12}$ | C． | $\frac{7\sqrt{3}}{12}$ | D． | -$\frac{7\sqrt{3}}{12}$ |
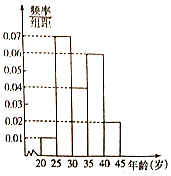今年我国许多省市雾霾频发，为增强市民的环境保护意识，某市面向全市学校征召100名教师做义务宣传志愿者，成立环境保护宣传组，现把该组的成员按年龄分成5组：第一组[20，25），第2组[25，30），第3组[30，35），第4组[35，40），第5组[40，45），得到的频率分布直方图如图所示．