题目内容
方程log2（x+4）-2x=0的一个根在区间[m，m+1]内，另一根在在区间[n，n+1]内，m，n∈Z，则m+n的值为 ．
考点：函数的零点与方程根的关系
专题：函数的性质及应用
分析：令f（x）=log2（x+4）-2x ，则由题意利用函数零点的判定定理可得函数f（x）在区间（-3，-2）内有一个零点，在区间（1，2）内有一个零点，由此求得m、n的值，可得m+n的值．
解答：
解：令f（x）=log2（x+4）-2x ，则由题意可得f（x）的零点
一个在区间[m，m+1]内，另一在在区间[n，n+1]内，m，n∈Z．
再根据f（-3）=0-
=-
＜0，f（-2）=1-
=
，可得函数f（x）在区间（-3，-2）内有一个零点．
再根据 f（1）=log25-2＞0，f（2）=log26-4＜0，可得函数f（x）在区间（1，2）内有一个零点．
故有m=-3，n=1，∴m+n=-2，
故答案为：-2．
一个在区间[m，m+1]内，另一在在区间[n，n+1]内，m，n∈Z．
再根据f（-3）=0-
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 4 |
| 3 |
| 4 |
再根据 f（1）=log25-2＞0，f（2）=log26-4＜0，可得函数f（x）在区间（1，2）内有一个零点．
故有m=-3，n=1，∴m+n=-2，
故答案为：-2．
点评：本题主要考查函数的零点与方程的根的关系，函数零点的判定定理，体现了转化的数学思想，属于基础题．
练习册系列答案
相关题目
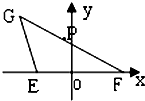已知E、F是x轴上的点，坐标原点O为线段EF的中点，G、P是坐标平面上的动点，点P在线段FG上，|