题目内容
20.已知函数f(x)=sin2x+mcos2x的图象关于直线x=$\frac{π}{8}$对称,则f(x)在区间[0,π]的单调递增区间为[0,$\frac{π}{8}$]和[$\frac{5π}{8}$,π]分析 依题意,f(0)=f($\frac{π}{4}$),可求得m=1,利用辅助角公式可得f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$),从而可求得f(x)的单调递增区间.
解答 解:∵函数f(x)=sin2x+mcos2x的图象关于直线x=$\frac{π}{8}$对称,
∴f(0)=f($\frac{π}{4}$),
∴m=1,
∴f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$),
由2kπ-$\frac{π}{2}$≤2x+$\frac{π}{4}$≤$\frac{π}{2}$+2kπ,k∈Z得:
kπ-$\frac{3π}{8}$≤x≤$\frac{π}{8}$+kπ,k∈Z.
又x∈[0,π],
∴f(x)在区间[0,π]的单调递增区间为[0,$\frac{π}{8}$]和[$\frac{5π}{8}$,π]
故答案为:[0,$\frac{π}{8}$]和[$\frac{5π}{8}$,π].
点评 本题考查正弦函数的单调性,考查y=Asin(ωx+φ)的图象与性质,考查分析与转化的能力,属于中档题.

练习册系列答案
相关题目
8.下列说法中不正确的是( )
| A. | 第一象限角可能是负角 | B. | -830°是第三象限角 | ||
| C. | 钝角一定是第二象限角 | D. | 相等角的终边与始边均相同 |
5.如果输入x=2,那么执行右图中算法的结果是( )


| A. | 输出2 | B. | 输出4 | ||
| C. | 输出8 | D. | 程序出错,输不出任何结果 |
12.扇形的中心角为120°,半径为2,则它的面积是( )
| A. | 240 | B. | 120 | C. | $\frac{2π}{3}$ | D. | $\frac{4π}{3}$ |
10.若点P(m-2,n+1),Q(n,m-1)关于直线l对称,则l的方程是( )
| A. | x-y+1=0 | B. | x-y=0 | C. | x+y+1=0 | D. | x+y=0 |
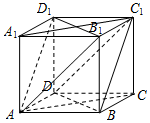 已知正方体ABCD-A1B1C1D1棱长为a.
已知正方体ABCD-A1B1C1D1棱长为a.