题目内容
12.扇形的中心角为120°,半径为2,则它的面积是( )| A. | 240 | B. | 120 | C. | $\frac{2π}{3}$ | D. | $\frac{4π}{3}$ |
分析 先利用弧长公式求弧长,再利用扇形的面积公式求面积.
解答 解:扇形的中心角为120°=$\frac{2π}{3}$,
∵半径为2,∴弧长为$\frac{4π}{3}$,
∴此扇形的面积为$\frac{1}{2}×\frac{4π}{3}×2$=$\frac{4π}{3}$.
故选:D.
点评 本题考查扇形的弧长与面积的计算,正确运用公式是关键,属于基础题.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
3.已知关于x的一元二次不等式ax2+bx+c>0的解集为{x|-2<x<3},则不等式cx2-bx+a<0的解集是( )
| A. | {x|x$<-\frac{1}{2}$或x$>\frac{1}{3}$} | B. | {x|x$\frac{1}{3}$或x>$\frac{1}{2}$} | C. | {x|-$\frac{1}{2}$<x<$\frac{1}{3}$} | D. | {x|-$\frac{1}{3}$<x<$\frac{1}{2}$} |
1.不等式$\frac{2-x}{x+4}$>1的解集是( )
| A. | (-∞,-1) | B. | (-4,2) | C. | (-4,-1) | D. | (-4,+∞) |
2.若函数f(x)=x2+(π-a)x,g(x)=cos(2x+a)则下列结论正确的是( )
| A. | ?a∈R,函数f(x)和g(x)都是奇函数 | B. | ?a∈R,函数f(x)和g(x)都是奇函数 | ||
| C. | ?a∈R,函数f(x)和g(x)都是偶函数 | D. | ?a∈R,函数f(x)和g(x)都是偶函数 |
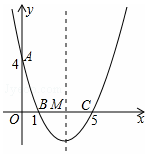 如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x 轴相交于点M.
如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x 轴相交于点M.