题目内容
15．下列关于实数a，b的不等式中，不恒成立的是（ ）| A． | a2+b2≥2ab | B． | a2+b2≥-2ab | C． | ${（{\frac{a+b}{2}}）^2}≥ab$ | D． | ${（{\frac{a+b}{2}}）^2}≥-ab$ |
分析 根据级别不等式的性质分别判断即可．
解答 解：对于A：a2+b2-2ab=（a-b）2≥0，故A恒成立；
对于B：a2+b2+2ab=（a+b）2≥0，故B恒成立；
对于C：${（\frac{a+b}{2}）}^{2}$-ab=${（\frac{a-b}{2}）}^{2}$≥0，故C恒成立；D不恒成立；
故选：D．
点评 本题考查了基本不等式的性质，是一道基础题．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
6．已知$\overrightarrow a=（λ+1，0，2λ）$，$\overrightarrow b=（6，2μ-1，2）$，若$\overrightarrow a⊥\overrightarrow b$，则λ的值为（ ）
| A． | $\frac{3}{5}$ | B． | $-\frac{3}{5}$ | ||
| C． | $-\frac{1}{10}$ | D． | 不确定，与μ值相关 |
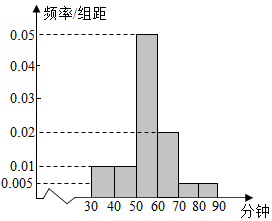某学校高二年级共有女生300人，现调查她们每天的课外运动时间，发现她们的课外运动时间介于30分钟到90分钟之间，如图是统计结果的频率分布直方图，则她们的平均运动时间大约是56.5分钟．