题目内容
10.已知函数$f(x)=cos({2x-\frac{π}{3}})+2sin({x-\frac{π}{4}})sin({x+\frac{π}{4}})$.(1)求函数y=f(x)在区间$[{-\frac{π}{12},\frac{π}{2}}]$上的最值;
(2)设△ABC的内角A、B、C的对边分别为a、b、c,满足$c=\sqrt{3}$,f(C)=1,且sinB=2sinA,求a、b的值.
分析 (1)展开两角和与差的正弦、余弦,然后利用辅助角公式化积,结合x的范围求得函数的最值;
(2)由f(C)=1求得C值,再由正弦定理把已知等式化角为边,结合余弦定理求得a、b的值.
解答 解:(1)∵$f(x)=cos({2x-\frac{π}{3}})+2sin({x-\frac{π}{4}})sin({x+\frac{π}{4}})$
=$\frac{1}{2}cos2x+\frac{\sqrt{3}}{2}sin2x+(sinx-cosx)(sinx+cosx)$
=$\frac{1}{2}cos2x+\frac{\sqrt{3}}{2}sin2x$+sin2x-cos2x
=$\frac{1}{2}cos2x+\frac{\sqrt{3}}{2}sin2x-cos2x$
=$sin(2x-\frac{π}{6})$.
∵$x∈[-\frac{π}{12},\frac{π}{2}]$,∴2x-$\frac{π}{6}$$∈[-\frac{π}{3},\frac{5π}{6}]$,
∴f(x)在2x-$\frac{π}{6}$=-$\frac{π}{3}$,即x=-$\frac{π}{12}$时,取最小值$-\frac{\sqrt{3}}{2}$;
在2x-$\frac{π}{6}$=$\frac{π}{2}$时,即x=$\frac{π}{3}$时,取最大值1;
(2)f(C)=sin(2C-$\frac{π}{6}$)=1,
∵0<C<π,0<2C<2π,
∴$-\frac{π}{6}<2C-\frac{π}{6}<\frac{11π}{6}$,则$2C-\frac{π}{6}=\frac{π}{2}$,C=$\frac{π}{3}$.
∵sinB=2sinA,
∴由正弦定理得:b=2a,①
由余弦定理得:${c}^{2}={a}^{2}+{b}^{2}-2ab•cos\frac{π}{3}$,
即c2=a2+b2-ab=3,②
解①②得:a=1,b=2.
点评 本题考查正弦定理和余弦定理的应用,考查了三角函数中的恒等变换应用,是中档题.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案 在一次文、理科学习倾向的调研中,对高一年段1000名学生进行文综、理综各一次测试(满分均为300分).测试后,随机抽取若干名学生成绩,记理综成绩X,文综成绩为Y,|X-Y|为Z,将Z值分组统计制成下表,并将其中女生的Z值分布情况制成频率分布直方图
在一次文、理科学习倾向的调研中,对高一年段1000名学生进行文综、理综各一次测试(满分均为300分).测试后,随机抽取若干名学生成绩,记理综成绩X,文综成绩为Y,|X-Y|为Z,将Z值分组统计制成下表,并将其中女生的Z值分布情况制成频率分布直方图值分布情况制成频率分布直方图(如图所示).
| 分组 | [0,20) | [20,40) | [40,60} | [60,80) | [80,100) | [100,120) | [120,140) |
| 频数 | 4 | 18 | 42 | 66 | 48 | 20 | 2 |
(Ⅱ)记Z的平均数为$\overline{Z}$,如果$\overline{Z}$>60称为整体具有学科学习倾向,试估计高一年段女生的$\overline{Z}$值(同一组中的数据用该组区间中点值作代表),并判断高一年段女生是否整体具有显著学科学习倾向.
| A. | {x|-1≤x≤1} | B. | {x|0≤x≤1} | C. | {x|0<x≤1} | D. | {x|0≤x<1} |
| A. | (0,2) | B. | [0,2] | C. | {0,2} | D. | {0,1,2} |
| A. | a2+b2≥2ab | B. | a2+b2≥-2ab | C. | ${({\frac{a+b}{2}})^2}≥ab$ | D. | ${({\frac{a+b}{2}})^2}≥-ab$ |
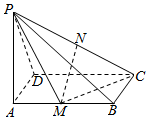 如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°.
如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°.