题目内容
7.将两名男生、两名女生发到三个不同的班取作经验交流,每个班至少分到一名学生,且两名女生不能分到同一个班,则不同的分法的种数为( )| A. | 18 | B. | 24 | C. | 30 | D. | 36 |
分析 由题意可以分两类,2名男生一组,两名女生各一组,或1名男生和一名女生一组,另外的一男一女各一组,根据分类计数原理可得.
解答 解:由题意可知,4人只能分为;2名男生一组,两名女生各一组,或1名男生和一名女生一组,另外的一男一女各一组,
故有A33(1+${C}_{2}^{1}{C}_{2}^{1}$)=30种,
故选:C.
点评 本题考查了分组分配问题,关键是分组,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知集合A={x||x-1|≤1,x∈R},${B}=\left\{{x\left|{\sqrt{x}≤2,x∈{Z}}\right.}\right\}$,则A∩B=( )
| A. | (0,2) | B. | [0,2] | C. | {0,2} | D. | {0,1,2} |
15.下列关于实数a,b的不等式中,不恒成立的是( )
| A. | a2+b2≥2ab | B. | a2+b2≥-2ab | C. | ${({\frac{a+b}{2}})^2}≥ab$ | D. | ${({\frac{a+b}{2}})^2}≥-ab$ |
2.已知a,b,c分别是△ABC中角A,B,C的对边长,b和c是关于x的方程x2-9x+25cosA=0的两个根(b>c),且$({sinB+sinC+sinA})({sinB+sinC-sinA})=\frac{18}{5}sinBsinC$,则△ABC的形状为( )
| A. | 等腰三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 钝角三角形 |
12.设点P(x0,y0)是函数y=tanx与y=-x(x≠0)的图象的一个交点,则(x02+1)(1+cos2x0)的值为( )
| A. | 2 | B. | 2+$\sqrt{2}$ | C. | 2+$\sqrt{3}$ | D. | 2-$\sqrt{2}$ |
16.下列说法正确的是( )
| A. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | 若a,b∈R,则“ab≠0”是“a≠0”的充分不必要条件 | |
| C. | 命题“?x0∈R,x02+x0+1<0”的否定是“?x∈R,x2+x+1>0” | |
| D. | 若“p且q”为假,则p,q全是假命题 |
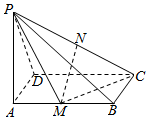 如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°.
如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°.