题目内容
已知F1，F2分别是双曲线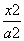
－
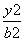＝1(a>0，b>0)的左、右焦点，P为双曲线上一点，若∠F1PF2＝90°，且△F1PF2的三边长成等差数列，则双曲线的离心率是( )
A．2 B．3
C．4 D．5
D
[解析] 设|PF1|＝m，|PF2|＝n，不妨设P在第一象限，则由已知得
∴5a2－6ac＋c2＝0，方程两边同除a2得，即e2－6e＋5＝0，解得e＝5或e＝1(舍去)，故选D.
练习册系列答案
相关题目
题目内容
已知F1，F2分别是双曲线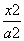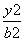－＝1(a>0，b>0)的左、右焦点，P为双曲线上一点，若∠F1PF2＝90°，且△F1PF2的三边长成等差数列，则双曲线的离心率是( )
A．2 B．3
C．4 D．5
D
[解析] 设|PF1|＝m，|PF2|＝n，不妨设P在第一象限，则由已知得
∴5a2－6ac＋c2＝0，方程两边同除a2得，即e2－6e＋5＝0，解得e＝5或e＝1(舍去)，故选D.
的定
义域
，则函数
的定义域为 
中，
分别是
和
的中点，求异面直线
与
所成角的大小 (结果用反三角函数值表示）.
＋
＝1(a>b>0)过点P(2,1)，且离心率e＝
.
，直线l与椭圆C交于A，B两点．求△PAB的面积的最大值．
与x轴所围的区域为D，若曲线y＝ax(x－2)(a<0)把D的面积均分为两等份，则a的值为( )
，向量c满足
，则
的值