题目内容
过函数y=x (0<x<1)图象上一点M作切线l与y轴和直线y=1分别交于点P,Q,点N(0,1),则△PQN面积的最大值为________.
(0<x<1)图象上一点M作切线l与y轴和直线y=1分别交于点P,Q,点N(0,1),则△PQN面积的最大值为________.

[解析] 设切点为M(t2,t),0<t<1,因为y′= ,所以切线斜率为k=
,所以切线斜率为k= ,切线方程为y-t=
,切线方程为y-t= (x-t2),即y=
(x-t2),即y= x+
x+ ,分别令x=0,y=1,得P
,分别令x=0,y=1,得P ,Q(2t-t2,1),所以△PQN的面积S=
,Q(2t-t2,1),所以△PQN的面积S=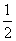
 (2t-t2)=
(2t-t2)= t3-t2+t,S′=
t3-t2+t,S′= t2-2t+1=
t2-2t+1= (t-2)(3t-2),注意到0<t<1,所以当t=
(t-2)(3t-2),注意到0<t<1,所以当t=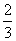 时,△PQN的面积取到最大值
时,△PQN的面积取到最大值 ×
× +
+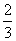 =
= .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 中,
中, 分别是
分别是 和
和 的中点,求异面直线
的中点,求异面直线 与
与 所成角的大小 (结果用反三角函数值表示).
所成角的大小 (结果用反三角函数值表示).
 与x轴所围的区域为D,若曲线y=ax(x-2)(a<0)把D的面积均分为两等份,则a的值为( )
与x轴所围的区域为D,若曲线y=ax(x-2)(a<0)把D的面积均分为两等份,则a的值为( )




 dx=________.
dx=________. 为等差数列,
为等差数列, 为等比数列,
为等比数列, ,
, ,则
,则 ( )
( ) D.
D. 

 ,向量c满足
,向量c满足 ,则
,则 的值
的值 上有一点P到左焦点的距离是4,则点p到右焦点的距离是( )
上有一点P到左焦点的距离是4,则点p到右焦点的距离是( )