题目内容
函数f（x）=（1+x）2-2ln（1+x）的单调增区间是 ．
考点：利用导数研究函数的单调性
专题：函数的性质及应用
分析：先求导数fˊ（x）然后在函数的定义域内解不等式fˊ（x）＞0和fˊ（x）＜0，fˊ（x）＞0的区间为单调增区间，fˊ（x）＜0的区间为单调减区间．
解答：
解：由x+1＞0，得：f（x）定义域为（-1，+∞），
又f′(x)=
，
∵x＞-1，∴x+1＞0且x+2＞0，
由f′（x）=0得x=0，
令f′（x）＞0得x＞0
∴增区间为（0，+∞）．
故答案为：（0，+∞）．
又f′(x)=
| 2x(x+2) |
| x+1 |
∵x＞-1，∴x+1＞0且x+2＞0，
由f′（x）=0得x=0，
令f′（x）＞0得x＞0
∴增区间为（0，+∞）．
故答案为：（0，+∞）．
点评：本题考查利用导数研究函数的单调性，属于基础题．
练习册系列答案
相关题目
已知O为空间直角坐标系的原点，以下能使向量
，
，
共面的三点A，B，C的坐标是（ ）
| OA |
| OB |
| OC |
| A、A（1，0，0），B（0，1，0），C（0，0，1） |
| B、A（1，2，3），B（3，0，2），C（4，2，5） |
| C、A（1，1，0），B（1，0，1），C（0，1，1） |
| D、A（1，1，1），B（1，1，0），C（1，0，1） |
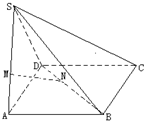如图，已知S是平行四边形ABCD所在平面外一点，M，N分别是SA，BD上的点，MN=5，AB=AD=SB=SA=6，且