题目内容
写出一个满足若x>y,则f(x)>f(y)且f(x+y)=2f(x)f(y)的函数f(x)= .
考点:抽象函数及其应用
专题:函数的性质及应用
分析:由条件:若x>y,则f(x)>f(y)知函数应为单调增函数;
由条件:若f(x+y)=2f(x)f(y),则函数应是指数类的函数,故考查函数f(x)=2x-1
由条件:若f(x+y)=2f(x)f(y),则函数应是指数类的函数,故考查函数f(x)=2x-1
解答:
解:考查函数f(x)=2x-1,
此函数单调递增,满足:若x>y,则f(x)>f(y);
又f(x+y)=2x+y-1=2×2x-12y-1=2f(x)f(y),
∴此函数满足f(x+y)=2f(x)f(y)
故答案为:f(x)=2x-1
此函数单调递增,满足:若x>y,则f(x)>f(y);
又f(x+y)=2x+y-1=2×2x-12y-1=2f(x)f(y),
∴此函数满足f(x+y)=2f(x)f(y)
故答案为:f(x)=2x-1
点评:本题主要考查了指数函数的运算性质的应用,属于基础试题

练习册系列答案
相关题目
在△ABC中,角A,B,C的对边分别是a,b,c,若a=2
,A=45°,B=60°,则b=( )
| 2 |
A、2
| ||
B、
| ||
| C、1 | ||
| D、2 |
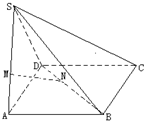 如图,已知S是平行四边形ABCD所在平面外一点,M,N分别是SA,BD上的点,MN=5,AB=AD=SB=SA=6,且
如图,已知S是平行四边形ABCD所在平面外一点,M,N分别是SA,BD上的点,MN=5,AB=AD=SB=SA=6,且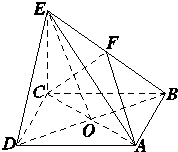 如图所示,在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
如图所示,在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.