题目内容
已知数列{an},其前n项和为sn,且sn=n2+n,则通项公式an= .
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由数列{an}的其前n项和sn求通项公式an时,通常先写出n≥2时sn-1的表达式,再求出an,并且验证n=1时an是否成立即可.
解答:
解:∵数列{an},其前n项和为sn,且sn=n2+n,
∴当n≥2时,sn-1=(n-1)2+(n-1),
∴an=sn-sn-1=(n2+n)-[(n-1)2+(n-1)]=2n;
当n=1时,a1=s1=1+1=2,满足an;
∴数列的通项公式为an=2n,n∈N*.
故答案为:2n,n∈N*.
∴当n≥2时,sn-1=(n-1)2+(n-1),
∴an=sn-sn-1=(n2+n)-[(n-1)2+(n-1)]=2n;
当n=1时,a1=s1=1+1=2,满足an;
∴数列的通项公式为an=2n,n∈N*.
故答案为:2n,n∈N*.
点评:本题考查了由数列{an}的其前n项和sn求通项公式an的问题,是基础题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知x4=81,那么x等于( )
| A、3 | B、-3 |
| C、-3或3 | D、不存在 |
已知某几何体的三视图如图所示,其中正(主)视图中半圆的半径为1,则该几何体的体积为( )
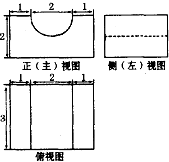

A、24-
| ||
B、24-
| ||
| C、24-π | ||
D、24-
|
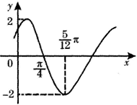 已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<