题目内容
若平面向量
,
的夹角为60°,且|
|=2|
|,则( )
| a |
| b |
| a |
| b |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点:数量积表示两个向量的夹角
专题:平面向量及应用
分析:由题意可得
•
=|
|2,再根据
•(
-
)=0,可得
⊥(
-
),从而得到答案.
| a |
| b |
| b |
| b |
| b |
| a |
| b |
| b |
| a |
解答:
解:由题意可得
•
=2|
|•|
|cos60°=|
|2,
∴
•(
-
)=
2-
•
=0,
∴
⊥(
-
),
故选:B.
| a |
| b |
| b |
| b |
| b |
∴
| b |
| b |
| a |
| b |
| a |
| b |
∴
| b |
| b |
| a |
故选:B.
点评:本题主要考查两个向量的数量积的定义,两个向量垂直的条件,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
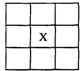 将1,1,2,2,2,3,3,3,3分别填入9个小方格中,每个小方格只填入一个数,每个数填入任何一个小方格是等可能的,则“3”填入图中标有“X”的小方格的概率是( )
将1,1,2,2,2,3,3,3,3分别填入9个小方格中,每个小方格只填入一个数,每个数填入任何一个小方格是等可能的,则“3”填入图中标有“X”的小方格的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
在平行四边形ABCD中,
+
等于( )
| AB |
| AD |
A、
| ||
B、
| ||
C、
| ||
D、|
|
双曲线
-
=1的焦距为( )
| x2 |
| 10 |
| y2 |
| 10 |
A、3
| ||
B、4
| ||
C、3
| ||
D、4
|
计算sin240°的值为( )
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
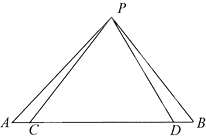 如图,C,D两点在△PAB的边AB上,AC=BD,若∠CPD=90°,且PA2+PB2=10,则2AB+CD的最大值为
如图,C,D两点在△PAB的边AB上,AC=BD,若∠CPD=90°,且PA2+PB2=10,则2AB+CD的最大值为