题目内容
已知M，N为平面区域
内的两个动点，向量
=（1，3），则当
∥
时，|
|2的最大值是（ ）
|
| a |
| MN |
| a |
| MN |
| A、4 | B、8 | C、20 | D、40 |
考点：简单线性规划
专题：不等式的解法及应用
分析：根据向量平行得到
所在直线的斜率k=3，进而得到对应直线的方程，利用数形结合即可得到结论．
| MN |
解答：
解：∵
∥
，
=（1，3），
∴
所在直线的斜率k=3，
设
所在的直线方程为y=3x+b，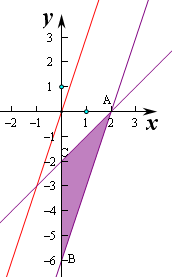
∵直线AB方程为3x-y+6=0，对应的斜率k=3，
∴平移直线y=3x+b，由图象可知当M，N位于A，B时，
此时，|
|最值，即|
|2最值，
∵A（2，0），B（0，-6），
∴|
|2=|AB|2=（2-0）2+（-6-0）2=4+36=40，
故选：D．
| MN |
| a |
| a |
∴
| MN |
设
| MN |
∵直线AB方程为3x-y+6=0，对应的斜率k=3，
∴平移直线y=3x+b，由图象可知当M，N位于A，B时，
此时，|
| MN |
| MN |
∵A（2，0），B（0，-6），
∴|
| MN |
故选：D．
点评：本题主要考查线性规划的应用，根据向量平行得到
所在直线的方程是解决本题的关键．
| MN |
练习册系列答案
直通贵州名校周测月考直通名校系列答案
培优三好生系列答案
相关题目
高三某班共有学生56人，其中女生24人，现用分层抽样的方法，选取14人参加一项活动，则应选取女生（ ）
| A、8人 | B、7人 | C、6人 | D、5人 |
若平面向量
，
的夹角为60°，且|
|=2|
|，则（ ）
| a |
| b |
| a |
| b |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
等比数列的前2项和为2，前4项和为10，则它的前6项和为（ ）
| A、31 | B、32 | C、41 | D、42 |
已知点A（0，1，2），B（2，3，4），|AB|=（ ）
A、2
| ||
B、3
| ||
C、
| ||
| D、12 |
