题目内容
16.已知F1,F2为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的交点,过F2作垂直于x轴的直线交双曲线于点P和Q,且△F1PQ为正三角形,则双曲线的渐近线方程为y=±$\sqrt{2}$x.分析 利用直角三角形中含30°角所对的边的性质及其双曲线的定义、勾股定理即可得到a,b的关系.
解答 解:∵在Rt△F1F2P中,∠PF1F2=30°,∴|PF1|=2|PF2|.
由双曲线定义知|PF1|-|PF2|=2a,∴|PF2|=2a,
由已知易得|F1F2|=$\sqrt{3}$|PF2|,∴2c=2$\sqrt{3}$a,∴c2=3a2=a2+b2,
∴2a2=b2,∵a>0,b>0,∴$\frac{b}{a}$=$\sqrt{2}$,故所求双曲线的渐近线方程为y=±$\sqrt{2}$x.
故答案为y=±$\sqrt{2}$x.
点评 熟练掌握双曲线的标准方程及其性质、等边三角形的性质等是解题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
7.已知函数y=f(x)的图象如图所示,则y=f(x)的解析式可能是( )


| A. | y=2x-x2-x | B. | y=$\frac{{2}^{x}sinx}{4x+1}$ | C. | y=(x2-2x)ex | D. | y=$\frac{x}{lnx}$ |
4.在平面直角坐标系xOy中,圆C的方程为x2+y2-8x+15=0,若直线y=kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的最大值是( )
| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | 3 |
1.将函数y=sin(2x+$\frac{π}{6}$)的图象向左平移$\frac{π}{3}$个单位,所得函数的解析式为( )
| A. | $y=sin({2x+\frac{5π}{6}})$ | B. | y=-cos2x | C. | y=cos2x | D. | $y=sin({2x-\frac{π}{6}})$ |
8.函数y=ln|x|-x2的图象大致为( )
| A. | 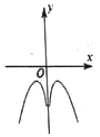 | B. | 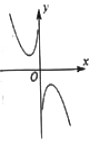 | C. |  | D. | 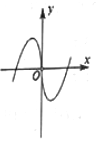 |
5.已知双曲线$\frac{{x}^{2}}{m}$-y2=1的一个焦点与抛物线y2=8x焦点相同,则此双曲线的离心率为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | 2 | D. | $\frac{2\sqrt{15}}{15}$ |