题目内容
20.焦距为10,短轴上顶点坐标为(12,0),(-12,0)的椭圆标准方程是$\frac{{y}^{2}}{169}$+$\frac{{x}^{2}}{144}$=1.分析 根据题意,分析可得要求椭圆中c=5,其焦点在y轴上,且b=12;由椭圆的性质可得a2的值,将a2、b2的值代入椭圆标准方程即可得答案.
解答 解:根据题意,椭圆的焦距为10,则2c=10,即c=5,
短轴上顶点坐标为(12,0),(-12,0),则其焦点在y轴上,且b=12;
则a2=b2+c2=169;
故椭圆的标准方程为:$\frac{{y}^{2}}{169}$+$\frac{{x}^{2}}{144}$=1;
故答案为:$\frac{{y}^{2}}{169}$+$\frac{{x}^{2}}{144}$=1.
点评 本题考查椭圆的标准方程,注意由短轴的顶点坐标判断出焦点的位置.

练习册系列答案
相关题目
10.下列函数在其定义域内既是奇函数又是减函数的是( )
| A. | y=-x3,x∈R | B. | y=lg|x|,x≠0 | C. | y=x+$\frac{1}{x}$,x≠0 | D. | y=($\frac{1}{2}$)x,x∈R |
15.读如图的程序,程序运行的结果是( )


| A. | 3 | B. | 7 | C. | 13 | D. | 21 |
5.从一批产品中取出三件产品,设A={三件产品全不是次品},B={三件产品全是次品},C={三件产品至少有一件是次品},则下列结论正确的是( )
| A. | A与C互斥 | B. | A与B互为对立事件 | ||
| C. | B与C互斥 | D. | 任何两个均互斥 |
9.“α是第一象限角”是“关于x,y的方程x2sinα+y2cosα=1所表示的曲线是椭圆”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |

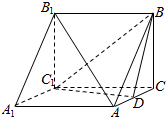 在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,BC⊥AC,BC=AC=2,AA1=3,D为棱AC的中点.
在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,BC⊥AC,BC=AC=2,AA1=3,D为棱AC的中点.