题目内容
12.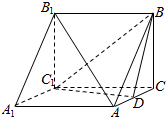 在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,BC⊥AC,BC=AC=2,AA1=3,D为棱AC的中点.
在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,BC⊥AC,BC=AC=2,AA1=3,D为棱AC的中点.(1)求证:AB1∥平面BDC1;
(2)求直线AB1与平面BCC1B1所成角的正切值.
分析 (1)连结B1C交BC1于E,连结DE,则DE∥AB1,由此能证明AB1∥平面BDC1.
(2)取AA1⊥底面ABC,推导出∠AB1C为直线AB1与平面BCC1B1所成角,由此能求出直线AB1与平面BCC1B1所成角的正切值.
解答 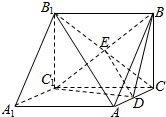 证明:(1)连结B1C交BC1于E,连结DE,
证明:(1)连结B1C交BC1于E,连结DE,
在三棱柱ABC-A1B1C1中,E是BC1的中点,
∵D为AC中点,∴DE∥AB1,
∵DE?面BDC1,AB1?面BDC1,
∴AB1∥平面BDC1.
解:(2)取AA1⊥底面ABC,AA1∥CC1,
∴CC1⊥底面ABC,∴CC1⊥AC,
∵BC⊥AC,∴AC⊥平面BCC1B1,
∴AB1在面BCC1B1的射影为B1C,
∴∠AB1C为直线AB1与平面BCC1B1所成角,
而B1C=$\sqrt{4+9}$=$\sqrt{13}$,AC=2,
在Rt△ACB1中,tan∠AB1C=$\frac{AC}{{B}_{1}C}$=$\frac{2\sqrt{13}}{13}$.
∴直线AB1与平面BCC1B1所成角的正切值为$\frac{2\sqrt{13}}{13}$.
点评 本题考查线面平行的证明,考查线面角的正切值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
3.2015年9月3日,抗战胜利70周年纪念活动在北京隆重举行,受到全国人民的瞩目.纪念活动包括举行纪念大会、阅兵式、招待会和文艺晚会等,据统计,抗战老兵由于身体原因,参加纪念大会、阅兵式、招待会这三个环节(可参加多个,也可都不参加)的情况及其概率如表所示:
(Ⅰ)若从抗战老兵中随机抽取2人进行座谈,求这2人参加纪念活动的环节数不同的概率;
(Ⅱ)某医疗部门决定从这些抗战老兵中(其中参加纪念活动的环节数为3的抗战老兵数大于等于3)随机抽取3名进行体检,设随机抽取的这3名抗战老兵中参加三个环节的有ξ名,求ξ的分布列和数学期望.
| 参加纪念活动的环节数 | 0 | 1 | 2 | 3 |
| 概率 | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{6}$ | $\frac{1}{6}$ |
(Ⅱ)某医疗部门决定从这些抗战老兵中(其中参加纪念活动的环节数为3的抗战老兵数大于等于3)随机抽取3名进行体检,设随机抽取的这3名抗战老兵中参加三个环节的有ξ名,求ξ的分布列和数学期望.
7.已知m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )
| A. | 若m?α,n?α,m∥β,n∥β,则α∥β | B. | 若m?α,m∥β,α∩β=n,则m∥n | ||
| C. | 若α∥β,m∥α,则m∥β | D. | 若m⊥n,n⊥β,β⊥α,则m⊥α |
2.如图为某几何体的三视图,则该几体的体积为( )
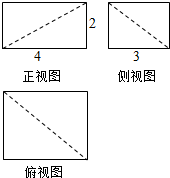

| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
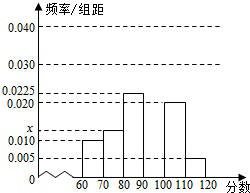 为了调查某校2000名高中生的体能情况,从中随机选取m名学生进行体能测试,将得到的成绩分成[60,70),[70,80),…,[110,120]六个组,并作出如下频率分布直方图,已知第四组的频数为12,图中从左到右的第一、二个矩形的面积比为4:5.规定:成绩在[60,70)、[70,90)、[90,110)、[110,120)的分别记为“不合格”、“合格”、“良好”,“优秀”,根据图中的信息,回答下列问题.
为了调查某校2000名高中生的体能情况,从中随机选取m名学生进行体能测试,将得到的成绩分成[60,70),[70,80),…,[110,120]六个组,并作出如下频率分布直方图,已知第四组的频数为12,图中从左到右的第一、二个矩形的面积比为4:5.规定:成绩在[60,70)、[70,90)、[90,110)、[110,120)的分别记为“不合格”、“合格”、“良好”,“优秀”,根据图中的信息,回答下列问题.