题目内容
10.椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上任意两点P,Q,若OP⊥OQ,则乘积|OP|•|OQ|的最小值为$\frac{2{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}$.分析 题意可设点P(|OP|cosθ,|OP|sinθ),Q(|OQ|cos(θ±$\frac{π}{2}$,|OQ|sin(θ±$\frac{π}{2}$),由P、Q在椭圆上,即可得出结论.
解答 解:题意可设点P(|OP|cosθ,|OP|sinθ),Q(|OQ|cos(θ±$\frac{π}{2}$,|OQ|sin(θ±$\frac{π}{2}$),
由P、Q在椭圆上,得:$\frac{1}{|OP{|}^{2}}$=$\frac{co{s}^{2}θ}{{a}^{2}}$+$\frac{si{n}^{2}θ}{{b}^{2}}$,①
$\frac{1}{|OQ{|}^{2}}$=$\frac{si{n}^{2}θ}{{a}^{2}}$+$\frac{co{s}^{2}θ}{{b}^{2}}$,②
①+②,得 $\frac{1}{|OP{|}^{2}}$+$\frac{1}{|OQ{|}^{2}}$=$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$,
∴当|OP|=|OQ|=$\sqrt{\frac{2{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}}$时,乘积|OP|•|OQ|最小值为$\frac{2{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}$.
故答案为:$\frac{2{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}$.
点评 本题考查椭圆中两线段乘积的最小值的求法,是中档题,解题时要认真审题,注意椭圆性质的合理运用.

练习册系列答案
相关题目
18.若命题p:?x0∈R,x02+x0+1<0,则¬p为( )
| A. | ?x∈R,x2+x+1<0 | B. | ?x∈R,x2+x+1>0 | C. | ?x∈R,x2+x+1≥0 | D. | ?x∈R,x2+x+1≥0 |
5.同时抛掷两枚骰子,向上点数之和为5的概率是( )
| A. | $\frac{1}{9}$ | B. | $\frac{2}{21}$ | C. | $\frac{1}{18}$ | D. | $\frac{1}{6}$ |
2.如图为某几何体的三视图,则该几体的体积为( )
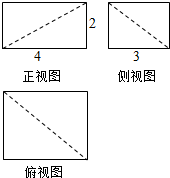

| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
20.已知a=ln$\frac{3}{4}$,b=5lg3,c=3${\;}^{-\frac{1}{2}}$,则a,b,c的大小关系为( )
| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | b<c<a |