题目内容
8.为促进抚州市精神文明建设,评选省级文明城市,现省检查组决定在未来连续5天中随机选取2天对抚州的各项文明建设进行暗访,则这两天恰好为连续两天的概率$\frac{2}{5}$.分析 先求出基本事件总数,再用列举法求出这两天恰好为连续两天包含怕基本事件个数,由此能求出这两天恰好为连续两天的概率.
解答 解:在未来连续5天中随机选取2天,基本事件总数为n=${C}_{5}^{2}$=10,
这两天恰好为连续两天包含的基本事件为(12),(23),(34),(45),共有4个基本事件,
∴这两天恰好为连续两天的概率p=$\frac{4}{10}=\frac{2}{5}$.
故答案为:$\frac{2}{5}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
19.过原点的直线与双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)交于M,N两点,P是双曲线上异于M,N的一点,若直线MP与直线NP的斜率都存在且乘积为$\frac{5}{4}$,则双曲线的离心率为( )
| A. | $\frac{3}{2}$ | B. | $\frac{9}{4}$ | C. | $\frac{5}{4}$ | D. | 2 |
16.阅读如图的算法框图,输出的结果S的值为( )
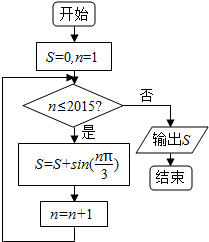

| A. | $\frac{{\sqrt{3}}}{2}$ | B. | 0 | C. | $\sqrt{3}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
3.2015年9月3日,抗战胜利70周年纪念活动在北京隆重举行,受到全国人民的瞩目.纪念活动包括举行纪念大会、阅兵式、招待会和文艺晚会等,据统计,抗战老兵由于身体原因,参加纪念大会、阅兵式、招待会这三个环节(可参加多个,也可都不参加)的情况及其概率如表所示:
(Ⅰ)若从抗战老兵中随机抽取2人进行座谈,求这2人参加纪念活动的环节数不同的概率;
(Ⅱ)某医疗部门决定从这些抗战老兵中(其中参加纪念活动的环节数为3的抗战老兵数大于等于3)随机抽取3名进行体检,设随机抽取的这3名抗战老兵中参加三个环节的有ξ名,求ξ的分布列和数学期望.
| 参加纪念活动的环节数 | 0 | 1 | 2 | 3 |
| 概率 | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{6}$ | $\frac{1}{6}$ |
(Ⅱ)某医疗部门决定从这些抗战老兵中(其中参加纪念活动的环节数为3的抗战老兵数大于等于3)随机抽取3名进行体检,设随机抽取的这3名抗战老兵中参加三个环节的有ξ名,求ξ的分布列和数学期望.
13.某几何体的三视图如图所示.则该几何体的外接球的表面积为( )


| A. | 8π | B. | 16π | C. | 32π | D. | 64π |
18.若命题p:?x0∈R,x02+x0+1<0,则¬p为( )
| A. | ?x∈R,x2+x+1<0 | B. | ?x∈R,x2+x+1>0 | C. | ?x∈R,x2+x+1≥0 | D. | ?x∈R,x2+x+1≥0 |