题目内容
9．“α是第一象限角”是“关于x，y的方程x2sinα+y2cosα=1所表示的曲线是椭圆”的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
分析 根据充分条件和必要条件的定义结合椭圆的方程进行判断即可．
解答 解：若x2sinα+y2cosα=1表示的曲线是椭圆，
则满足sinα＞0，cosα＞0，且sinα≠cosα，
即2kπ＜α＜2kπ+$\frac{π}{2}$，且α≠2kπ+$\frac{π}{4}$，k∈Z，
则“α是第一象限角”是“关于x，y的方程x2sinα+y2cosα=1所表示的曲线是椭圆”必要不充分条件，
故选：B
点评 本题主要考查充分条件和必要条件的判断，结合椭圆的方程进行判断是解决本题的关键．
练习册系列答案
相关题目
19．过原点的直线与双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a＞0，b＞0）交于M，N两点，P是双曲线上异于M，N的一点，若直线MP与直线NP的斜率都存在且乘积为$\frac{5}{4}$，则双曲线的离心率为（ ）
| A． | $\frac{3}{2}$ | B． | $\frac{9}{4}$ | C． | $\frac{5}{4}$ | D． | 2 |
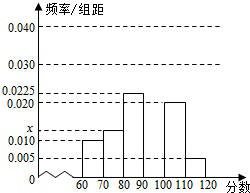为了调查某校2000名高中生的体能情况，从中随机选取m名学生进行体能测试，将得到的成绩分成[60，70），[70，80），…，[110，120]六个组，并作出如下频率分布直方图，已知第四组的频数为12，图中从左到右的第一、二个矩形的面积比为4：5．规定：成绩在[60，70）、[70，90）、[90，110）、[110，120）的分别记为“不合格”、“合格”、“良好”，“优秀”，根据图中的信息，回答下列问题．
18．若命题p：?x0∈R，x02+x0+1＜0，则￢p为（ ）
| A． | ?x∈R，x2+x+1＜0 | B． | ?x∈R，x2+x+1＞0 | C． | ?x∈R，x2+x+1≥0 | D． | ?x∈R，x2+x+1≥0 |