题目内容
10.下列函数在其定义域内既是奇函数又是减函数的是( )| A. | y=-x3,x∈R | B. | y=lg|x|,x≠0 | C. | y=x+$\frac{1}{x}$,x≠0 | D. | y=($\frac{1}{2}$)x,x∈R |
分析 根据奇函数、偶函数及函数单调性的定义,以及根据导数符号判断函数单调性的方法便可判断每个选项的函数的奇偶性和单调性,从而找出正确选项.
解答 解:A.y=-x3为奇函数,且x增大时,y减小;
∴该函数为定义域R上的减函数,∴该选项正确;
B.y=lg|x|为定义域{x|x≠0}上的偶函数,∴该选项错误;
C.$y′=\frac{{x}^{2}-1}{{x}^{2}}$;
∴x∈(-∞,-1),(1,+∞)时,y′>0,x∈(-1,1)时,y′<0;
∴函数y=$x+\frac{1}{x}$在定义域{x|x≠0}上没有单调性,∴该选项错误;
D.$y=(\frac{1}{2})^{x}$的图象不关于原点对称,不是奇函数,∴该选项错误.
故选:A.
点评 考查奇函数、偶函数的定义,减函数的定义,以及根据导数符号判断函数单调性的方法,奇函数图象的对称性,熟悉指数函数的图象.

练习册系列答案
相关题目
20.某几何体的三视图如图所示(单位:cm),则该几何体的表面积是( )
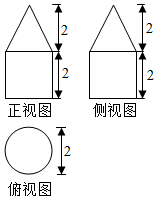

| A. | (5+$\sqrt{5}$)πcm2 | B. | (5+2$\sqrt{5}$)πcm2 | C. | (6+$\sqrt{5}$)πcm2 | D. | (6+2$\sqrt{5}$)πcm2 |
5.某几何体的三视图如图所示,则其体积为( )
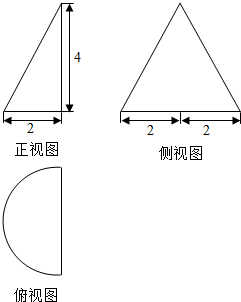

| A. | $\frac{4}{3}π$ | B. | $\frac{8}{3}π$ | C. | $\frac{16}{3}π$ | D. | $\frac{32}{3}π$ |
15.直线ax+by-a-b=0(a≠)与圆x2+y2-2=0的位置关系为( )
| A. | 相离 | B. | 相切 | C. | 相交或相切 | D. | 相交 |
19.过原点的直线与双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)交于M,N两点,P是双曲线上异于M,N的一点,若直线MP与直线NP的斜率都存在且乘积为$\frac{5}{4}$,则双曲线的离心率为( )
| A. | $\frac{3}{2}$ | B. | $\frac{9}{4}$ | C. | $\frac{5}{4}$ | D. | 2 |