题目内容
3.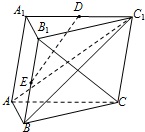 如图,在三棱柱ABC-A1B1C1中,D,E分别为A1C1,BB1的中点,B1C⊥AB,侧面BCC1B1为菱形.求证:
如图,在三棱柱ABC-A1B1C1中,D,E分别为A1C1,BB1的中点,B1C⊥AB,侧面BCC1B1为菱形.求证:(Ⅰ)DE∥平面ABC1;
(Ⅱ)B1C⊥DE.
分析 (Ⅰ)取AA1的中点F,连DF,FE.由DF∥AC1,EF∥AB.可证DF∥平面ABC1.同理根据线面平行的判定定理可证EF∥平面ABC1,可证平面DEF∥平面ABC1,即可证明DE∥平面ABC1.
(Ⅱ)由B1C⊥BC1.又B1C⊥AB,可证B1C⊥平面ABC1.即可证明B1C⊥平面DEF,从而可证B1C⊥DE.
解答  解:(Ⅰ)如图,取AA1的中点F,连DF,FE.又因为D,E分别为A1C1,BB1的中点,
解:(Ⅰ)如图,取AA1的中点F,连DF,FE.又因为D,E分别为A1C1,BB1的中点,
所以DF∥AC1,EF∥AB.
因为DF?平面ABC1,AC1?平面ABC1,
故DF∥平面ABC1.…(3分)
同理,EF∥平面ABC1.
因为DF,EF为平面DEF内的两条相交直线,
所以平面DEF∥平面ABC1.…(5分)
因为DE?平面DEF,所以DE∥平面ABC1.…(7分)
(Ⅱ)因为三棱柱ABC-A1B1C1的侧面BCC1B1为菱形,
故B1C⊥BC1.…(9分)
又B1C⊥AB,且AB,BC1为平面ABC1内的两条相交直线,
所以B1C⊥平面ABC1.…(12分)
而平面DEF∥平面ABC1,所以B1C⊥平面DEF,
因为DE?平面DEF,
所以B1C⊥DE.…(14分)
点评 本题主要考查空间直线和平面平行以及面面垂直的判定,考查了空间想象能力和推理论证能力,利用相应的判定定理是解决本题的关键,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.已知定义在R上的函数y=f(x)对任意的x都满足f(x+2)=f(x),当-1≤x<1时,f(x)=x3.若函数g(x)=f(x)-loga|x|恰有6个不同零点,则a的取值范围是( )
| A. | ($\frac{1}{7}$,$\frac{1}{5}$]∪(5,7] | B. | ($\frac{1}{5}$,$\frac{1}{3}$]∪(5,7] | C. | ($\frac{1}{5}$,$\frac{1}{3}$]∪(3,5] | D. | ($\frac{1}{7}$,$\frac{1}{5}$]∪(3,5] |
13.已知m>n>0,x是m、n的等差中项,y是m、n的等比中项,则x,y的大小关系是( )
| A. | x>y | B. | x=y | ||
| C. | x<y | D. | 大小不确定,与m、n的取值有关 |

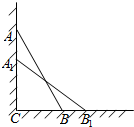 如图,一根木棒AB长为2米,斜靠在墙壁AC上,∠ABC=60°,若AB滑动至A1B1位置,且$A{A_1}=(\sqrt{3}-\sqrt{2})$米,则①BB1=$\sqrt{2}$-1米;②木棒AB的中点D所经过的路程为$\frac{π}{12}$米.
如图,一根木棒AB长为2米,斜靠在墙壁AC上,∠ABC=60°,若AB滑动至A1B1位置,且$A{A_1}=(\sqrt{3}-\sqrt{2})$米,则①BB1=$\sqrt{2}$-1米;②木棒AB的中点D所经过的路程为$\frac{π}{12}$米.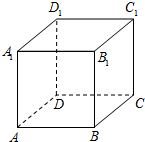 如图,已知正方体ABCD-A1B1C1D,若在其12条棱中随机地取3条,则这三条棱两两是异面直线的概率是$\frac{2}{55}$(结果用最简分数表示)
如图,已知正方体ABCD-A1B1C1D,若在其12条棱中随机地取3条,则这三条棱两两是异面直线的概率是$\frac{2}{55}$(结果用最简分数表示)