题目内容
已知椭圆C的中心在原点,离心率为
,短轴在y轴上且长度大于1,定点A(0,
)到椭圆C点的最远距离为
,求椭圆的标准方程.
| ||
| 2 |
| 3 |
| 2 |
| 7 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设椭圆的标准方程为
+
=1(2a>2b>1).由
=
可得a=2b.椭圆的方程可化为x2+4y2=4b2.设椭圆C上的任意一点P(x,y).可得|PA|2=x2+(y-
)2=-3(y+
)2+4b2+3.由于b>
,利用二次函数的单调性即可得出.
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| a |
| ||
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:设椭圆的标准方程为
+
=1(2a>2b>1).
由
=
可得1-
=
,解得a=2b.
∴椭圆的方程可化为x2+4y2=4b2.
设椭圆C上的任意一点P(x,y).
|PA|2=x2+(y-
)2=4b2-4y2+y2-3y+
=-3(y+
)2+4b2+3.
∵2b>1,∴b>
,
∴当y=-
时,|PA|取得最大值
.
∴4b2+3=7,解得b=1.
∴椭圆的标准方程为
+y2=1.
| x2 |
| a2 |
| y2 |
| b2 |
由
| c |
| a |
| ||
| 2 |
| b2 |
| a2 |
| 3 |
| 4 |
∴椭圆的方程可化为x2+4y2=4b2.
设椭圆C上的任意一点P(x,y).
|PA|2=x2+(y-
| 3 |
| 2 |
| 9 |
| 4 |
| 1 |
| 2 |
∵2b>1,∴b>
| 1 |
| 2 |
∴当y=-
| 1 |
| 2 |
| 7 |
∴4b2+3=7,解得b=1.
∴椭圆的标准方程为
| x2 |
| 4 |
点评:本题考查了椭圆的标准方程及其性质、两点之间的距离公式、二次函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
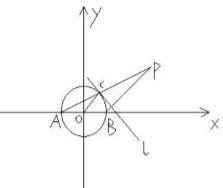 已知A,B是⊙0:x2+y2=4与x轴的两个交点,C是⊙O上异于点A,B的任意一点,过点B作直线l的垂线BP,且与AC的延长线交于点P,求点P的轨迹方程.
已知A,B是⊙0:x2+y2=4与x轴的两个交点,C是⊙O上异于点A,B的任意一点,过点B作直线l的垂线BP,且与AC的延长线交于点P,求点P的轨迹方程.