题目内容
在区间[0,10]上任取一个实数a,使得不等式2x2-ax+8≥0在(0,+∞)上恒成立的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:应用题,概率与统计
分析:不等式2x2-ax+8≥0在(0,+∞)上恒成立,则△=a2-64≤0,可得-8≤a≤8,求出区间[0,10]上构成的区域长度,再求出在区间[0,10]上任取一个数构成的区域长度,再求两长度的比值.
解答:
解:∵不等式2x2-ax+8≥0在(0,+∞)上恒成立,
∴△=a2-64≤0,
∴-8≤a≤8,
∵在区间[0,10]上任取一个实数a,
∴使得不等式2x2-ax+8≥0在(0,+∞)上恒成立的概率为
=
.
故选:D.
∴△=a2-64≤0,
∴-8≤a≤8,
∵在区间[0,10]上任取一个实数a,
∴使得不等式2x2-ax+8≥0在(0,+∞)上恒成立的概率为
| 8 |
| 10 |
| 4 |
| 5 |
故选:D.
点评:本题主要考查概率的建模和解模能力,本题是长度类型,思路是先求得试验的全部构成的长度和构成事件的区域长度,再求比值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列给出的赋值语句中正确的是( )
| A、3=A | B、x=-x |
| C、B=A=2 | D、x+y=0 |
若0<x<y<1,则( )
| A、3y<3x | ||||
B、(
| ||||
| C、logx3<logy3 | ||||
D、x-
|
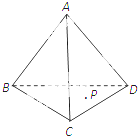 如图,在四面体A-BCD中,△BCD是正三角形,侧棱AB、AC、AD两两垂直且相等,设P为四面体A-BCD表面(含棱)上的一点,由点P到四个顶点的距离组成的集合记为M,如果集合M中有且只有2个元素,那么符合条件的点P有( )
如图,在四面体A-BCD中,△BCD是正三角形,侧棱AB、AC、AD两两垂直且相等,设P为四面体A-BCD表面(含棱)上的一点,由点P到四个顶点的距离组成的集合记为M,如果集合M中有且只有2个元素,那么符合条件的点P有( )| A、4个 | B、6个 | C、8个 | D、14个 |
已知抛物线x2=y+1上一定点A(-1,0)和两动点P、Q,当PA⊥PQ时,点Q的横坐标的取值范围( )
| A、(-∞,-3]∪[1,+∞) |
| B、[1,+∞) |
| C、[-3,-1] |
| D、(-∞,-3] |
在抛物线y2=4x上恒有两点关于直线l:y=kx+3则对称,k的取值范围是( )
| A、-1<k<0 |
| B、0<k<1 |
| C、-1≤k≤0 |
| D、0≤k≤1 |
设变量x、y满足约束条件
,则z=2x+3y的最大值为( )
|
| A、18 | B、2 | C、3 | D、0 |