题目内容
8.设变量x,y满足约束条件$\left\{\begin{array}{l}x+2y≤5\\ 2x+y≤4\\ x≥0\\ y≥0\end{array}\right.$,则目标函数z=3x+2y的最大值为7.分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案.
解答 解:由约束条件$\left\{\begin{array}{l}x+2y≤5\\ 2x+y≤4\\ x≥0\\ y≥0\end{array}\right.$作出可行域如图,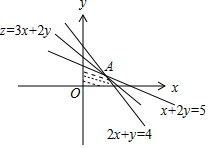
联立$\left\{\begin{array}{l}{x+2y=5}\\{2x+y=4}\end{array}\right.$,解得A(1,2).
化目标函数z=3x+2y为$y=-\frac{3}{2}x+\frac{z}{2}$,由图可知,当直线$y=-\frac{3}{2}x+\frac{z}{2}$过A时,
直线在y轴上的截距最大,z有最大值为7.
故答案为:7.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
13.设集合$A=\left\{{x\left|{\frac{2x+1}{x-2}≤0}\right.}\right\}$,B={x|x<1},则A∪B=( )
| A. | $[{-\frac{1}{2},1})$ | B. | (-1,1)∪(1,2) | C. | (-∞,2) | D. | $[{-\frac{1}{2},2})$ |
17.执行如图所示的程序框图,若输入m=4,t=3,则输出y=( )


| A. | 183 | B. | 62 | C. | 61 | D. | 184 |
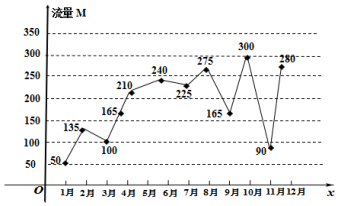 某人的手机使用的是每月300M流量套餐,如图记录了某人在去年1月到12月的流量使用情况.其中横轴代表月份,纵轴代表流量.
某人的手机使用的是每月300M流量套餐,如图记录了某人在去年1月到12月的流量使用情况.其中横轴代表月份,纵轴代表流量.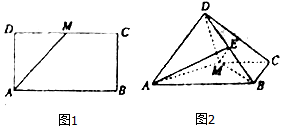 如图,已知长方形ABCD中,AB=2AD,M为DC的中点,将△ADM沿AM折起,使得平面ADM⊥平面ABCM.
如图,已知长方形ABCD中,AB=2AD,M为DC的中点,将△ADM沿AM折起,使得平面ADM⊥平面ABCM.