题目内容
下列结论正确的是（ ）
| A、命题：“若sinα=sinβ，则α=β”是真命题 | ||||||||
| B、若函数f（x）可导，且在x=x0处有极值，则f′（x0）=0 | ||||||||
C、向量
| ||||||||
| D、命题P：“?x∈R，ex＞x+1”的否定是“?x∈R，ex＜x+1” |
考点：命题的真假判断与应用
专题：简易逻辑
分析：举例说明A、C错误；由极值点处的导数等于0说明B正确；写出命题的否定说明D错误．
解答：
解：sin30°=sin150°，但30°≠150°，∴选项A错误；
若函数f（x）可导，且在x=x0处有极值，则f′（x0）=0，∴B正确；
当向量
，
的夹角为180°时，
•
＜0，∴C错误；
命题P：“?x∈R，ex＞x+1”的否定是“?x∈R，ex≤x+1”，∴D错误．
故选：B．
若函数f（x）可导，且在x=x0处有极值，则f′（x0）=0，∴B正确；
当向量
| a |
| b |
| a |
| b |
命题P：“?x∈R，ex＞x+1”的否定是“?x∈R，ex≤x+1”，∴D错误．
故选：B．
点评：本题考查了命题的真假判断与运用，考查了函数的极值与导数的关系，考查了平面向量的数量积，是基础题．
练习册系列答案
相关题目
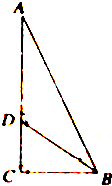
如图，已知直角三角形ACB中，∠C=90°，D为AC上一点，且
=2
，∠ABD=30°，则cos∠ADB=（ ）
| AD |
| DC |
A、-
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
不等式|x-1|+|x+3|≤6的解集为（ ）
| A、[-4，2] |
| B、[2，+∞） |
| C、（-∞，-4] |
| D、（-∞，-4]∪[2，+∞） |
数列{an}，已知a1=2，an+1=1-
（n∈N*），则a2014等于（ ）
| 1 |
| an |
| A、-1 | ||
B、-
| ||
C、
| ||
| D、2 |
如图所示，由函数f（x）=sinx与函数g（x）=cosx在区间[0，| 3π |
| 2 |
A、3
| ||
B、4
| ||
C、
| ||
D、2
|
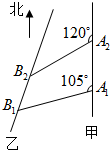如图，甲船以每小时15