题目内容
某家具厂有方木料9m2,五合板60m2,准备加工成书桌和书橱出售,已知生产每张书桌需方木料0.1m3,五合板2m2;生产每个书橱需方木料0.2m3,五合板1m2,出售一张书桌可获利40元,出售一张书橱可获利60元,问怎样安排生产可使获利最大?
考点:简单线性规划
专题:不等式的解法及应用
分析:根据条件建立约束条件和目标函数,利用线性规划的知识进行求解即可.
解答:
 解:设生产书桌x张,书橱y个,可获利润z元.
解:设生产书桌x张,书橱y个,可获利润z元.
则由题意可知
,
目标函数为z=40x+60y
作出可行域如图,
由
,
得A(10,40),
由上图可知最优解为(10,40),所以当生产书桌10张,书橱40个时获得的利润最大.
 解:设生产书桌x张,书橱y个,可获利润z元.
解:设生产书桌x张,书橱y个,可获利润z元.则由题意可知
|
目标函数为z=40x+60y
作出可行域如图,
由
|
得A(10,40),
由上图可知最优解为(10,40),所以当生产书桌10张,书橱40个时获得的利润最大.
点评:本题主要考查与不等式有关的应用问题,利用条件建立不等式关系,结合线性规划的知识是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
不等式|x-1|+|x+3|≤6的解集为( )
| A、[-4,2] |
| B、[2,+∞) |
| C、(-∞,-4] |
| D、(-∞,-4]∪[2,+∞) |
 如图所示,由函数f(x)=sinx与函数g(x)=cosx在区间[0,
如图所示,由函数f(x)=sinx与函数g(x)=cosx在区间[0,| 3π |
| 2 |
A、3
| ||
B、4
| ||
C、
| ||
D、2
|
某公司共有工作人员200人,其中职员160人,中级管理人员30人,高级管理人员10人,现要从中抽取20个人进行身体健康检查,如果采取分层抽样的方法,则职员、中级管理人员和高级管理人员各应抽取的人数为( )
| A、16,3,1 |
| B、16,2,2 |
| C、8,15,7 |
| D、12,3,5 |
同样规格的黑、白两色正方形瓷砖铺设的若干图案,则按此规律,设第n个图案中黑色瓷砖数为an,白色瓷砖数为bn,则
=( )
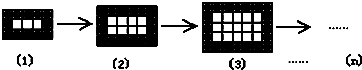
| a40 |
| b40 |
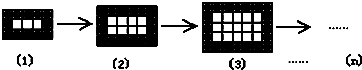
A、
| ||
B、
| ||
C、
| ||
D、
|
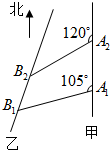 如图,甲船以每小时15
如图,甲船以每小时15