题目内容
给定k∈N*,设函数f:N*→N*满足:对于任意大于k的正整数n,f(n)=n-k.已知命题:k=3,当n≤3且n∈N*时,2≤f(n)≤3为真命题,则不同的函数f的个数为 .
考点:映射
专题:函数的性质及应用
分析:当k=3时,f(n)=n-3,然后根据2≤f(n)≤3,确定函数的个数.
解答:
解:∵n≤3,k=3,2≤f(n)≤3,
∴f(1)=2或3,且 f(2)=2或3 且 f(3)=2或3.
根据分步计数原理,可得共2×2×2=8个不同的函数.
故答案为:8
∴f(1)=2或3,且 f(2)=2或3 且 f(3)=2或3.
根据分步计数原理,可得共2×2×2=8个不同的函数.
故答案为:8
点评:本题主要考查映射的定义,以及分步计数原理的应用,比较基础.

练习册系列答案
相关题目
不等式|x-1|+|x+3|≤6的解集为( )
| A、[-4,2] |
| B、[2,+∞) |
| C、(-∞,-4] |
| D、(-∞,-4]∪[2,+∞) |
同样规格的黑、白两色正方形瓷砖铺设的若干图案,则按此规律,设第n个图案中黑色瓷砖数为an,白色瓷砖数为bn,则
=( )
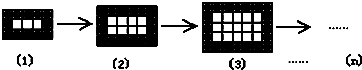
| a40 |
| b40 |
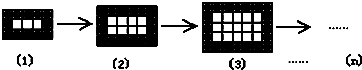
A、
| ||
B、
| ||
C、
| ||
D、
|
定义在R上的偶函数f(x)满足:对任意的x1,x2∈(-∞,0](x1≠x2),都有(x2-x1)•[f(x2)-f(x1)]>0,则( )
| A、f(-2)<f(1)<f(3) |
| B、f(1)<f(-2)<f(3) |
| C、f(3)<f(-2)<f(1) |
| D、f(3)<f(1)<f(-2) |
已知球的半径为2,相互垂直的两个平面分别截球面得两个圆,若两圆的公共弦长为2,则两圆的圆心距等于C( )
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
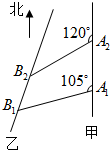 如图,甲船以每小时15
如图,甲船以每小时15