题目内容
某商店如果将进货为8元的商品按每件10元售出，每天可销售200件，现在采用提高售价，减少进货量的方法增加利润，已知这种商品每涨价0.5元，其销售量就减少10件，问应该将售价定为多少时，才能使所赚利润最大，并求出最大利润．
考点：函数解析式的求解及常用方法,函数的最值及其几何意义
专题：函数的性质及应用
分析：设每件销售价提高x元，由题意可得所获利润：y=（2+x）•（200-20x），由二次函数的知识可得结论．
解答：
解：设每件销售价提高x元，则每件利润（2+x）元
每天销售量变为（200-20x）件
所获利润：y=（2+x）•（200-20x）
即y=-20x2+160x+400
配方得y=-20（x-4）2+720
由二次函数的知识可知当x=4，
即售价定为14元时，每天可获得最大利润720元．
每天销售量变为（200-20x）件
所获利润：y=（2+x）•（200-20x）
即y=-20x2+160x+400
配方得y=-20（x-4）2+720
由二次函数的知识可知当x=4，
即售价定为14元时，每天可获得最大利润720元．
点评：本题考查函数解析式的求解，以及二次函数的最值，属基础题．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
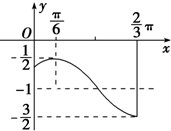如图，是函数y=Asin（ωx+φ）+k（A＞0，ω＞0，|φ|＜
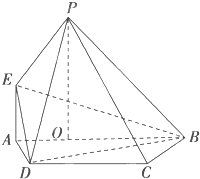如图，PO⊥平面ABCD，点O在AB上，EA∥PO，四边形ABCD为直角梯形，BC⊥AB，BC=CD=BO=PO，EA=AO=