题目内容
已知集合A={1，4，a2-2a}，B={a-2，a2-4a+2，a2-3a+3，a2-5a}，A∩B={1，3}，则A∪B= ．
考点：交集及其运算,并集及其运算
专题：集合
分析：由A∩B={1，3}得到a2-2a=3，解得：a=-1或a=3．然后分a=-1或a=3讨论，求出B，则A∪B可求．
解答：
解：∵A={1，4，a2-2a}，B={a-2，a2-4a+2，a2-3a+3，a2-5a}，且A∩B={1，3}，
∴a2-2a=3，解得：a=-1或a=3．
当a=-1时，a-2=-3，a2-4a+2=7，a2-3a+3=7，a2-5a=6．
集合B违背集合中元素的互异性；
当a=3时，a-2=1，a2-4a+2=-1，a2-3a+3=3，a2-5a=-6．
B={1，-1，3，-6}．
A∪B={1，-1，3，4，-6}．
故答案为：{1，-1，3，4，-6}．
∴a2-2a=3，解得：a=-1或a=3．
当a=-1时，a-2=-3，a2-4a+2=7，a2-3a+3=7，a2-5a=6．
集合B违背集合中元素的互异性；
当a=3时，a-2=1，a2-4a+2=-1，a2-3a+3=3，a2-5a=-6．
B={1，-1，3，-6}．
A∪B={1，-1，3，4，-6}．
故答案为：{1，-1，3，4，-6}．
点评：本题考查了交集、并集的运算，考查了集合中元素的特性，是基础题．
练习册系列答案
相关题目
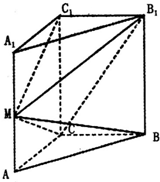如图，在直三棱柱ABC-A1B1C1中，∠ACB=90°，2AC=AA1=BC=2，M为AA1的中点．