题目内容
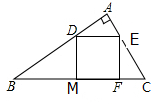 如图,正方形DEFM内接于△ABC,且点D,E在AB,AC上,点F,M在BC上,∠A=90°,S△CEF=1,S△BMD=4,求S△ABC.
如图,正方形DEFM内接于△ABC,且点D,E在AB,AC上,点F,M在BC上,∠A=90°,S△CEF=1,S△BMD=4,求S△ABC.考点:相似三角形的性质
专题:立体几何
分析:由已知可得△CEF∽△DBM∽△EDA∽△CAB,结合S△CEF=1,S△BMD=4,可得这些三角形两直角边长的比例,进而求出S△ABC.
解答:
解:∵正方形DEFM内接于△ABC,∠A=90°,
可得△CEF∽△DBM∽△EDA∽△CAB,
设CF=x,由S△CEF=1,S△BMD=4,
可得:CF:DM=1:2,
故FE=DE=2x,
即
x•2x=1,即x=1,
故CE=
,AE=
,
故AC=
,则AB=
,
故S△ABC=
AC•AB=
可得△CEF∽△DBM∽△EDA∽△CAB,
设CF=x,由S△CEF=1,S△BMD=4,
可得:CF:DM=1:2,
故FE=DE=2x,
即
| 1 |
| 2 |
故CE=
| 5 |
| ||
| 5 |
故AC=
6
| ||
| 5 |
12
| ||
| 5 |
故S△ABC=
| 1 |
| 2 |
| 36 |
| 5 |
点评:本题考查的知识是相似三角形的性质,三角形求面积,难度不大,属于基础题.

练习册系列答案
相关题目
 某工厂对一批产品进行了抽样检测.如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )
某工厂对一批产品进行了抽样检测.如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )| A、90 | B、75 | C、60 | D、45 |
在棱长为6的正方体ABCD-A1B1C1D1中,M是BC的中点,点P是面DCC1D1所在的平面内的动点,且满足∠APD=∠MPC,则三棱锥P-BCD的体积最大值是( )
| A、36 | ||
B、12
| ||
| C、24 | ||
D、18
|
已知正数组成的等比数列{an},若a1•a20=100,那么a7+a14的最小值为( )
| A、20 | B、25 | C、50 | D、不存在 |
下列函数中,图象关于y轴对称的是( )
| A、y=log2x |
| B、y=x3 |
| C、y=cosx |
| D、y=sinx |