题目内容
已知函数f(x)=loga(x-1),a>0且a≠1.
(1)求函数f(x)的定义域和零点;
(2)若f(3)>0,且f(2m-1)>f(4-m),求实数m的取值范围.
(1)求函数f(x)的定义域和零点;
(2)若f(3)>0,且f(2m-1)>f(4-m),求实数m的取值范围.
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:(1)先求出函数的定义域,令函数值为0,解出即可;
(2)先求出函数是增函数,根据f(2m-1)>f(4-m),得出不等式组,解出即可.
(2)先求出函数是增函数,根据f(2m-1)>f(4-m),得出不等式组,解出即可.
解答:
解:(1)函数f(x)的定义域是(1,+∞),
令
=0,解得:x=2,
∴函数的零点是2;
(2)∵f(3)>0,∴
>0,∴a>1,
∴函数f(x)=
是增函数,
∵f(2m-1)>f(4-m),
∴
,
解得:
<m<3.
令
| log | (x-1) a |
∴函数的零点是2;
(2)∵f(3)>0,∴
| log | 2 a |
∴函数f(x)=
| log | (x-1) a |
∵f(2m-1)>f(4-m),
∴
|
解得:
| 5 |
| 3 |
点评:本题考查了对数函数的性质,考查了函数的单调性,是一道基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
若函数f(x)在R上是单调递减的奇函数,则下列关系式成立的是( )
| A、f(3)<f(4) |
| B、f(3)<-f(-4) |
| C、-f(-3)<f(-4) |
| D、f(-3)>f(-4) |
函数f(x)=2sin(
-
)+1(x∈R)的最小正周期、最大值依次为( )
| x |
| 2 |
| π |
| 3 |
| A、4π,3 | B、4π,2 |
| C、2π,3 | D、2π,2 |
函数f(x)=2sin(2x+
)在区间(-π,π)上零点的个数为( )
| π |
| 3 |
| A、5 | B、4 | C、3 | D、2 |
若对实数a和b,定义运算“⊕”:a⊕b=(a+b)×(a-3b),则当x∈[1,8]时,(log2x)⊕1的最大值和最小值分别为( )
| A、-3,0 |
| B、0,-4 |
| C、-4,不存在 |
| D、-3,不存在 |

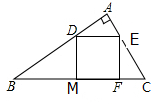 如图,正方形DEFM内接于△ABC,且点D,E在AB,AC上,点F,M在BC上,∠A=90°,S△CEF=1,S△BMD=4,求S△ABC.
如图,正方形DEFM内接于△ABC,且点D,E在AB,AC上,点F,M在BC上,∠A=90°,S△CEF=1,S△BMD=4,求S△ABC.